题目内容
已知幂函数y=f(x)的图象过点(2,
).
(1)求y=f(x)的解析式;
(2)判断y=f(x)在其定义域上的单调性,丙加以证明.
| 2 |
(1)求y=f(x)的解析式;
(2)判断y=f(x)在其定义域上的单调性,丙加以证明.
考点:幂函数的性质,幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:(1)设幂函数f(x)=xα,把点(4,2)代入求出α的值,即可求出函数的解析式;
(2)先判断出函数的单调性,利用单调性的定义法:取值、作差、变形、定号、下结论进行证明.
(2)先判断出函数的单调性,利用单调性的定义法:取值、作差、变形、定号、下结论进行证明.
解答:
解:(1)设幂函数f(x)=xα,
因为幂函数的图象经过点(2,
),
所以2α=
,解得α=
,
则幂函数的解析式为f(x)=
;
(2)函数f(x)=
在定义域[0,+∞)上为增函数,
证明如下:
任取x1、x2∈[0,+∞),且x1<x2,
则f(x1)-f(x2)=
-
=
=
,
∵0≤x1<x2,∴x1-x2<0,且
+
>0,
∴
<0,即f(x1)-f(x2)<0,
则f(x1)<f(x2),
所以函数f(x)=
在定义域[0,+∞)上为增函数.
因为幂函数的图象经过点(2,
| 2 |
所以2α=
| 2 |
| 1 |
| 2 |
则幂函数的解析式为f(x)=
| x |
(2)函数f(x)=
| x |
证明如下:
任取x1、x2∈[0,+∞),且x1<x2,
则f(x1)-f(x2)=
| x1 |
| x2 |
(
| ||||||||
|
| x1-x2 | ||||
|
∵0≤x1<x2,∴x1-x2<0,且
| x1 |
| x2 |
∴
| x1-x2 | ||||
|
则f(x1)<f(x2),
所以函数f(x)=
| x |
点评:本题考查待定系数法求出幂函数的解析式,以及单调性的定义法:取值、作差、变形、定号、下结论进行证明函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)在(-∞,-1]上是增函数,则下列关系式中成立的是( )
A、f(-
| ||
B、f(-1)<f(-2)<f(-
| ||
C、f(-2)<f(-1)<f(-
| ||
D、f(-2)<f(-
|
在△ABC中,已知tanC=
,c=8,则△ABC外接圆的半径为( )
| 4 |
| 3 |
| A、5 | B、6 | C、8 | D、10 |
若正数x,y满足
+
=1,则3x+4y的最小值是( )
| 3 |
| 5x |
| 1 |
| 5y |
A、
| ||
| B、5 | ||
C、
| ||
| D、6 |
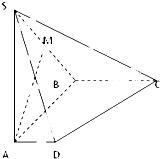 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点.