题目内容
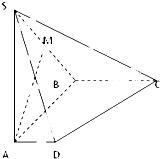如图，在四棱锥S-ABCD中，侧棱SA⊥底面ABCD，AD∥BC，∠ABC=90°，SA=AB=BC=2，AD=1．M是棱SB的中点．（1）求证：AM∥面SCD；
（2）设点N是线段CD上的一点，且
| AN |
| AD |
考点：直线与平面平行的判定
专题：空间位置关系与距离,空间角
分析：（1）根据已知条件容易发现，取BC中点E，连接AE，ME，则能够证明平面AME∥平面SCD，所以AM∥面SCD；
（2）先找到MN与面SAB所成的角θ，根据已知条件，过N作NF∥AD，则NF⊥平面SAB，连接MF，MN，则∠FMN=θ，而sinθ=
，而根据已知条件知NF=a．所以根据条件求出MN即可，可以用a来表示MN．分别延长BA，CD相交于G，则有：
=
，所以可求出GA=2，而根据
=
，可以用a表示出BF，这时候在△MBF中可根据余弦定理求出MF，所以在Rt△MNF中，可求出MN，即用a表示出MN=
，所以sinθ=
=
，显然当
=
，即a=
时，sinθ最大．
（2）先找到MN与面SAB所成的角θ，根据已知条件，过N作NF∥AD，则NF⊥平面SAB，连接MF，MN，则∠FMN=θ，而sinθ=
| NF |
| MN |
| GA |
| GA+2 |
| 1 |
| 2 |
| a |
| 2 |
| 2+2-FB |
| 4 |
| 5a2-12a+10 |
| a | ||
|
|
| 1 |
| a |
| 3 |
| 5 |
| 5 |
| 3 |
解答：
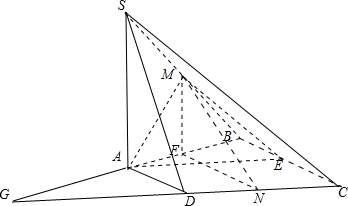
解：（1）证明：如图，取BC中点E，连接AE，ME，则：
ME∥SC，CE=1；
∵AD=1，AD∥CE；
∴四边形ADCE是平行四边形；
∴AE∥CD；
又SC，CD?平面SCD，ME，AE?平面SCD；
∴ME∥平面SCD，AE∥平面SCD，ME∩AE=E；
∴平面AME∥平面SCD，AM?平面AME；
∴AM∥平面SCD；
（2）过N作NF∥AD；
∵SA⊥底面ABCD，∴SA⊥AD，即AD⊥SA；
又AD⊥AB，SA∩AB=A；
∴AD⊥平面SAB；
∴NF⊥平面SAB；
连接MF，MN，则：∠FMN是MN与面SAB所成的角；
∴∠FMN=θ；
由题意知NF=a，延长BA交CD延长线于G，则：
=
；
∴GA=2；
由
=
得：
=
；
∴FB=4-2a；
在△MBF中，∠MBF=45°，BM=
，FB=4-2a，由余弦定理得：
MF2=FB2+BM2-2FB•BM•cos45°=4a2-12a+10；
∴在Rt△MNF中，MN=
；
∴sinθ=
=
=
=
；
∴
=
，即a=
时，sinθ取最大值
．
ME∥SC，CE=1；∵AD=1，AD∥CE；
∴四边形ADCE是平行四边形；
∴AE∥CD；
又SC，CD?平面SCD，ME，AE?平面SCD；
∴ME∥平面SCD，AE∥平面SCD，ME∩AE=E；
∴平面AME∥平面SCD，AM?平面AME；
∴AM∥平面SCD；
（2）过N作NF∥AD；
∵SA⊥底面ABCD，∴SA⊥AD，即AD⊥SA；
又AD⊥AB，SA∩AB=A；
∴AD⊥平面SAB；
∴NF⊥平面SAB；
连接MF，MN，则：∠FMN是MN与面SAB所成的角；
∴∠FMN=θ；
由题意知NF=a，延长BA交CD延长线于G，则：
| GA |
| GA+2 |
| 1 |
| 2 |
∴GA=2；
由
| NF |
| BC |
| GF |
| GB |
| a |
| 2 |
| 4-FB |
| 4 |
∴FB=4-2a；
在△MBF中，∠MBF=45°，BM=
| 2 |
MF2=FB2+BM2-2FB•BM•cos45°=4a2-12a+10；
∴在Rt△MNF中，MN=
| 5a2-12a+10 |
∴sinθ=
| a | ||
|
| 1 | ||||||
|
| 1 | ||||||||
|
| 1 | ||||||||
|
∴
| 1 |
| a |
| 3 |
| 5 |
| 5 |
| 3 |
| ||
| 7 |
点评：考查线面平行的判定定理，面面平行的判定定理，面面平行的性质，以及余弦定理，配方法求二次函数的最值．
练习册系列答案
相关题目
若0＜m＜n＜1，则（ ）
| A、3n＜3m | ||||
| B、logm4＜logn4 | ||||
| C、log5m＜log5n | ||||
D、(
|
已知全集U={1，2，3，4，5}，A={1，3，5}，则∁UA=（ ）
| A、{1，2} |
| B、{2，4，5} |
| C、{2，3，4} |
| D、{2，4} |
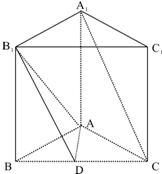如图，底面是正三角形的直三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=2．