题目内容
6.执行如图所示的程序框图,若输出k的值为8,则判断框内可填入的条件是( )
| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{15}{24}$ |
分析 模拟执行程序框图,依次写出每次循环得到的k,S的值,当S>$\frac{11}{12}$时,退出循环,输出k的值为8,故判断框图可填入的条件是S≤$\frac{11}{12}$.
解答 解:模拟执行程序框图,k的值依次为0,2,4,6,8,
因此S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$=$\frac{11}{12}$(此时k=6),
因此可填:S≤$\frac{11}{12}$.
故选:C.
点评 本题考查了当型循环结构的程序框图,根据框图的流程判断程序运行的S值是解题的关键,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如表:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.
| 甲 | 29 | 37 | 35 | 33 | 26 | 50 |
| 乙 | 32 | 33 | 28 | 34 | 40 | 43 |
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.
17.集合M={x|0≤x<2},集合N={x|x2+2x-3<0},则集合M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
11.某人射击1次,命中8~10环的概率如表所示:
则他射击1次,至少命中9环的概率为0.3.
| 命中环数 | 10环 | 9环 | 8环 |
| 概 率 | 0.12 | 0.18 | 0.28 |
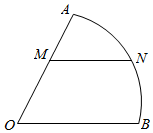 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.