题目内容
14.(Ⅰ)设z=1+i(i是虚数单位),求$\frac{2}{z}$+z2的值;(Ⅱ)设x,y∈R,复数z=x+yi,且满足|z|2+(z+$\overline{z}$)i=$\frac{3-i}{2+i}$,试求x,y的值.
分析 (Ⅰ)把z=1+i,代入$\frac{2}{z}$+z2,然后由复数代数形式的乘除运算化简得答案;
(Ⅱ)把Z=x+yi代入|z|2+(z+$\overline{z}$)i=$\frac{3-i}{2+i}$,整理后利用复数相等的条件列式求解x,y的值,则答案可求.
解答 解:(Ⅰ)由z=1+i(i是虚数单位),
则$\frac{2}{z}$+z2=$\frac{2}{1+i}+(1+i)^{2}=\frac{2(1-i)}{(1+i)(1-i)}+2i$=1-i+2i=1+i;
(Ⅱ)把z=x+yi代入|z|2+(z+$\overline{z}$)i=$\frac{3-i}{2+i}$,
得${x}^{2}+{y}^{2}+2xi=\frac{(3-i)(2-i)}{(2+i)(2-i)}=1-i$,
则$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{2x=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{\sqrt{3}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=-\frac{\sqrt{3}}{2}}\end{array}\right.$.
点评 本题考查了复数代数形式的乘除运算,考查了复数相等的条件,考查了复数的基本概念,是基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
5.已知f(x)=$\frac{1}{3}{x^3}$+2xf′(1),则f′(1)等于( )
| A. | 0 | B. | -1 | C. | 2 | D. | 1 |
2.已知集合M={x|x>0},N={x|x2≤4},则集合M∩N=( )
| A. | {x|-2<x<0} | B. | {x|0<x≤2} | C. | {x|-2<x<2} | D. | {x|x>-2} |
6.执行如图所示的程序框图,若输出k的值为8,则判断框内可填入的条件是( )

| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{15}{24}$ |
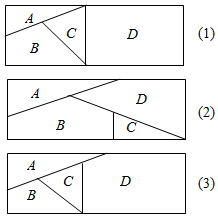 用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.
用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.