题目内容
13.已知θ为第二象限角,tan 2θ=-2$\sqrt{2}$.(1)求tan θ的值;
(2)求$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-tan\frac{5π}{4}}{\sqrt{2}sin(θ+\frac{π}{4})}$的值.
分析 (1)利用三角恒等变换,以及三角函数在各个象限中的符号,求得 tan θ的值.
(2)利用三角恒等变换,同角三角函数的基本关系,化简所给的式子,可得结果.
解答 解:(1)∵θ为第二象限角,∴tan θ<0,∵tan 2θ=$\frac{2tanθ}{1{-tan}^{2}θ}$=-2$\sqrt{2}$.
∴tan θ=-$\frac{\sqrt{2}}{2}$,或tanθ=$\sqrt{2}$(舍去).
(2)$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-tan\frac{5π}{4}}{\sqrt{2}sin(θ+\frac{π}{4})}$=$\frac{{2cos}^{2}\frac{θ}{2}-1-sinθ}{\sqrt{2}•(\frac{\sqrt{2}}{2}sinθ+\frac{\sqrt{2}}{2}cosθ)}$=$\frac{cosθ-sinθ}{cosθ+sinθ}$
=$\frac{1-tanθ}{1+tanθ}$=$\frac{1+\frac{\sqrt{2}}{2}}{1-\frac{\sqrt{2}}{2}}$=4+2$\sqrt{2}$.
点评 本题主要考查三角恒等变换,同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
10.已知圆C:x2+y2=4,直线l:y=x,则圆C上任取一点A到直线l的距离小于1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
4.已知向量$\overrightarrow{a}$=($\sqrt{3}$,-1),向量$\overrightarrow{b}$=(1+tcos$\frac{π}{5}$,tsin$\frac{π}{5}$)(t>0),则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角可能是( )
| A. | $\frac{π}{9}$ | B. | $\frac{5π}{18}$ | C. | $\frac{7π}{18}$ | D. | $\frac{11π}{18}$ |
8.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{169}$=1的焦点坐标为( )
| A. | (5,0),(-5,0) | B. | (0,5),(0,-5) | C. | (0,12),(0,-12) | D. | (12,0),(-12,0) |
2.某研究机构在对线性相关的两个变量x和y进行统计分析时,得到如下数据:
由表中数据求的y关于x的回归方程为$\hat y=0.65x+\hat a$,则在这些样本点中任取一点,该点落在回归直线下方的概率为( )
| x | 4 | 6 | 8 | 10 | 12 |
| y | 1 | 2 | 3 | 5 | 6 |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
3.某班5名学生的数学和物理成绩如表:
(1)画出散点图;
(2)求物理成绩y对数学成绩x的线性回归方程:
(3)一名学生的数学成绩为96分,试预测他的物理成绩.
参考数据:$\sum_{i=1}^5{{x_i}{y_i}}=25054,\sum_{i=1}^5{{x_i}^2}=27174$.
| 学生 学科 | A | B | C | D | E |
| 数学成绩(x) | 88 | 76 | 73 | 66 | 63 |
| 物理成绩(y) | 78 | 65 | 71 | 64 | 61 |
(2)求物理成绩y对数学成绩x的线性回归方程:
(3)一名学生的数学成绩为96分,试预测他的物理成绩.
参考数据:$\sum_{i=1}^5{{x_i}{y_i}}=25054,\sum_{i=1}^5{{x_i}^2}=27174$.
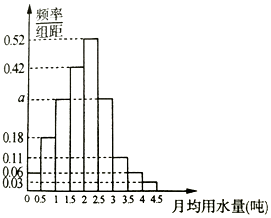 我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.