题目内容
已知函数f(x)=log2(x2-x),g(x)=log2(ax-a).
(Ⅰ)求f(x)的定义域;
(Ⅱ)若g(x)的定义域为(1,+∞),求当f(x)>g(x)时x的取值范围.
(Ⅰ)求f(x)的定义域;
(Ⅱ)若g(x)的定义域为(1,+∞),求当f(x)>g(x)时x的取值范围.
考点:对数函数的定义域
专题:函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)由对数的真数大于0,求出f(x)的定义域;
(Ⅱ)由g(x)的定义域求出a的取值范围,由f(x)>g(x),得出不等式x2-x>ax-a,从而求出x的取值范围.
(Ⅱ)由g(x)的定义域求出a的取值范围,由f(x)>g(x),得出不等式x2-x>ax-a,从而求出x的取值范围.
解答:
解:(Ⅰ)由题意,x2-x>0,
解得x<0,或x>1;
∴f(x)的定义域为{x|x<0,或x>1};…(4分)
(Ⅱ)∵g(x)=log2(ax-a),
∴ax-a>0,即a(x-1)>0;
又∵g(x)=log2(ax-a)的定义域为(1,+∞),
∴x-1>0,即所以a>0;…(6分)
当f(x)>g(x)时,x>1;
且x2-x>ax-a,即(x-1)(x-a)>0;
∴①当0<a≤1时,x>1;
②当a>1时,x>a.…(12分)
解得x<0,或x>1;
∴f(x)的定义域为{x|x<0,或x>1};…(4分)
(Ⅱ)∵g(x)=log2(ax-a),
∴ax-a>0,即a(x-1)>0;
又∵g(x)=log2(ax-a)的定义域为(1,+∞),
∴x-1>0,即所以a>0;…(6分)
当f(x)>g(x)时,x>1;
且x2-x>ax-a,即(x-1)(x-a)>0;
∴①当0<a≤1时,x>1;
②当a>1时,x>a.…(12分)
点评:本题考查了函数的性质与应用问题,也考查了利用函数的性质解不等式的问题,解题时应利用转化思想,把所求的问题转化为可以解答的问题,是基础题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
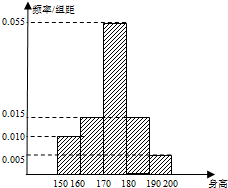 某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.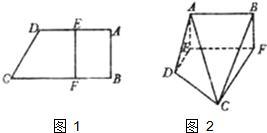 如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.
如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.