题目内容
某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥数不少于钾肥数,且不多于钾肥数的1.5倍.
(1)设买钾肥x吨,买氮肥y吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(2)设点P(x,y)在(1)中的可行域内,求t=
的取值范围.
(1)设买钾肥x吨,买氮肥y吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(2)设点P(x,y)在(1)中的可行域内,求t=
| y+20 |
| x-10 |
考点:简单线性规划的应用
专题:数形结合
分析:(1)题意得约束条件,画出可行域,数形结合的方法得到结果;(Ⅱ)t=
表示(Ⅰ)中可行域内动点P(x,y)与定点B(10,-20)连线的斜率,利用几何意义解决.
| y+20 |
| x-10 |
解答:
 解:(Ⅰ)设肥料总数为z,z=x+y,由题意得约束条件
解:(Ⅰ)设肥料总数为z,z=x+y,由题意得约束条件
,即
-----(2分)
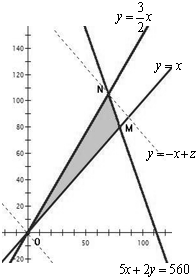
画出可行域(如图)-------(4分)
目标函数:z=x+y,即y=-x+z,
表示斜率为-1,y轴上截距为z的平行直线系.
当直线过点N时,z最大.
联立方程
,解得N(70,105)
此时zmax=x+y=70+105=175.∴购买钾肥70吨,氮肥105吨时,两种肥料的总数量最大为175吨------(7分)
(Ⅱ)t=
表示(Ⅰ)中可行域内动点P(x,y)与定点B(10,-20)连线的斜率.
联立方程
,解得M(80,80)kBO=
=-2,kNO=
=
,∴t∈(-∞,-2]∪[
,+∞)--------------(9分)
 解:(Ⅰ)设肥料总数为z,z=x+y,由题意得约束条件
解:(Ⅰ)设肥料总数为z,z=x+y,由题意得约束条件
|
|
画出可行域(如图)-------(4分)
目标函数:z=x+y,即y=-x+z,
表示斜率为-1,y轴上截距为z的平行直线系.
当直线过点N时,z最大.
联立方程
|
此时zmax=x+y=70+105=175.∴购买钾肥70吨,氮肥105吨时,两种肥料的总数量最大为175吨------(7分)
(Ⅱ)t=
| y+20 |
| x-10 |
联立方程
|
| -20-0 |
| 10-0 |
| 80-(-20) |
| 80-10 |
| 10 |
| 7 |
| 10 |
| 7 |
点评:本题考查的是线性规划中的应用问题,t=
的几何意义,数形结合是解决此类问题的关键.
| y+20 |
| x-10 |

练习册系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,且△ABC为正三角形,点D是BC的中点,BC=BB1.
在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,且△ABC为正三角形,点D是BC的中点,BC=BB1.