题目内容
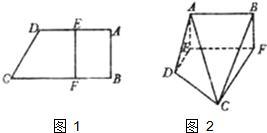 如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.
如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直. (1)判断直线AD与BC是否共面,并证明你的结论;
(2)当直线AC与面EFCD所成角的正切值为多少时,二面角A-DC-E的大小是60°?
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)利用反证法证明AD、BC是异面直线;(2)先证明∠AHE是二面角A-DC-E的平面角,再求∠AHE的正切值.
解答:
解:(1)AD、BC是异面直线,(1分)
(反证法)假设AD、BC共面为α.
∵EF⊥BC,∠ABC=90°,∴EF⊥AB,EF?α,AB?α.
∴EF⊥α,又EFCD∩α=CD∴EF⊥CD,∴CD⊥AB.
这与ABCD为梯形矛盾.故假设不成立.即AD、BC是异面直线.…(6分)
(2)延长CD,FE相交于N,由已知∴ED=2,CF=4设AB=x则△NDE中,NE=x,
∵AE⊥EF,平面ABFE平面EFCD,
∴AE⊥平面EFCD.过E作EH⊥DN于H,连结AH,
则AH⊥DN.∴∠AHE是二面角A-DC-E的平面角,
则∠AHE=60°.∵NE=x,DE=2,∴HE=
,AE=2,
∴tan∠AHE=
=
=
x2=2,x=
,
此时在△EFC中,EF=
,FC=4∴EC=3
.又AE⊥平面EFCD,
∴∠ACE是直线AC与平面EFCD所成的角,
∴tan∠ACE=
=
=
.
即当直线AC与平面EFCD所成角的正切值为
时,二面角A-DE-E的
大小为60°.
(反证法)假设AD、BC共面为α.
∵EF⊥BC,∠ABC=90°,∴EF⊥AB,EF?α,AB?α.
∴EF⊥α,又EFCD∩α=CD∴EF⊥CD,∴CD⊥AB.
这与ABCD为梯形矛盾.故假设不成立.即AD、BC是异面直线.…(6分)
(2)延长CD,FE相交于N,由已知∴ED=2,CF=4设AB=x则△NDE中,NE=x,
∵AE⊥EF,平面ABFE平面EFCD,
∴AE⊥平面EFCD.过E作EH⊥DN于H,连结AH,
则AH⊥DN.∴∠AHE是二面角A-DC-E的平面角,
则∠AHE=60°.∵NE=x,DE=2,∴HE=
| 2x | ||
|
∴tan∠AHE=
| AE |
| EH |
| ||
| x |
| 3 |
| 2 |
此时在△EFC中,EF=
| 2 |
| 2 |
∴∠ACE是直线AC与平面EFCD所成的角,
∴tan∠ACE=
| AE |
| EC |
| 2 | ||
3
|
| ||
| 3 |
即当直线AC与平面EFCD所成角的正切值为
| ||
| 3 |
大小为60°.
点评:本题考查的知识点是二面角的平面角及求法,异面直线的判定,其中(1)中反证法关键是由假设结论不成立,推理后得到矛盾,直接法是要熟练掌握异面直线的判定定理,(2)的关键是找出∠AHE是二面角A-DC-E的平面角,∠ACE是直线AC与平面EFCD所成的角.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目

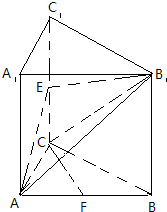 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2. 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD.