题目内容
在△ABC中,a、b、c分别是角A、B、C的对边,A=60°,B<C,b、c是方程x2-2
x+m=0的两个实根,△ABC的面积为
.
(1)求m的值;
(2)求△ABC的三边长.
| 3 |
| ||
| 2 |
(1)求m的值;
(2)求△ABC的三边长.
考点:解三角形
专题:计算题,解三角形
分析:(1)利用三角形的面积公式,结合韦达定理,求m的值;
(2)求出方程的根,可得b,c,利用余弦定理求出a,即可求△ABC的三边长.
(2)求出方程的根,可得b,c,利用余弦定理求出a,即可求△ABC的三边长.
解答:
解:(1)∵A=60°,△ABC的面积为
,
∴
bc•
=
,
∴bc=2,
∵b、c是方程x2-2
x+m=0的两个实根,
∴bc=m=2;
(2)∵b、c是方程x2-2
x+2=0的两个实根,B<C,
∴b=
-1,c=
+1,
∴a2=(
-1)2+(
+1)2-2×2×
=6,
∴a=
.
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴bc=2,
∵b、c是方程x2-2
| 3 |
∴bc=m=2;
(2)∵b、c是方程x2-2
| 3 |
∴b=
| 3 |
| 3 |
∴a2=(
| 3 |
| 3 |
| 1 |
| 2 |
∴a=
| 6 |
点评:本题考查三角形面积的计算,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
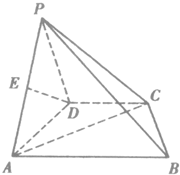 如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.