题目内容
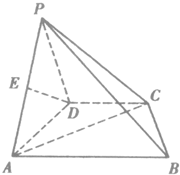 如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.(1)求证:CD⊥PA;
(2)求证:DE∥平面PBC.
考点:直线与平面平行的判定,棱锥的结构特征,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)根据线面垂直的性质定理即可得到结论.
(2)根据线面平行的判定定理即可证明DE∥平面PBC
(2)根据线面平行的判定定理即可证明DE∥平面PBC
解答:
 证明:(1)∵AD⊥AB,CD∥AB,
证明:(1)∵AD⊥AB,CD∥AB,
∴CD⊥AD…(2分)
又∵侧面PAD与底面ABCD垂直且交线为AD,
∴CD垂直侧面PAD…(4分)
又∵PA?平面PAD∴CD⊥PA…(6分)
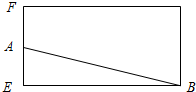
(2)如图,取AB的中点F,连结DF,EF,
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,
∴BF∥CD,且BF=CD,
则四边形BCDF为平行四边形,
则DF∥BC,
∵BC?平面PBC,DF?平面PBC,
∴DF∥平面PBC.
在△PAB中,PE=EA,AF=FB,
∴EF∥PB.…(9分)
又∵PB?平面PBC,EF?平面PBC
∴EF∥平面PBC.
又∵DFEF=F,
∴平面DEF∥平面PBC.…(11分)
∵DE?平面DEF,
∴DE∥平面PBC.…(12分)
证法二:取PB的中点M,边CM,EM
在△PAB中,PE=EA,PM=MB,
∴EM∥AB,EM=
AB…(8分)
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,
∴CD=
AB,CD∥AB
∴EM
CD…(9分)
∴四边形CDEM为平行四边形,
∴DE∥CM.…(10分)
又∵CM?平面PBC,DE?平面PBC
∴DE∥平面PBC…(12分)
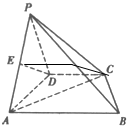
 证明:(1)∵AD⊥AB,CD∥AB,
证明:(1)∵AD⊥AB,CD∥AB,∴CD⊥AD…(2分)
又∵侧面PAD与底面ABCD垂直且交线为AD,
∴CD垂直侧面PAD…(4分)
又∵PA?平面PAD∴CD⊥PA…(6分)
(2)如图,取AB的中点F,连结DF,EF,
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,
∴BF∥CD,且BF=CD,
则四边形BCDF为平行四边形,
则DF∥BC,
∵BC?平面PBC,DF?平面PBC,

∴DF∥平面PBC.
在△PAB中,PE=EA,AF=FB,
∴EF∥PB.…(9分)
又∵PB?平面PBC,EF?平面PBC
∴EF∥平面PBC.
又∵DFEF=F,
∴平面DEF∥平面PBC.…(11分)
∵DE?平面DEF,
∴DE∥平面PBC.…(12分)
证法二:取PB的中点M,边CM,EM
在△PAB中,PE=EA,PM=MB,
∴EM∥AB,EM=
| 1 |
| 2 |
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,
∴CD=
| 1 |
| 2 |
∴EM
| ||
. |
∴四边形CDEM为平行四边形,
∴DE∥CM.…(10分)
又∵CM?平面PBC,DE?平面PBC
∴DE∥平面PBC…(12分)

点评:本题主要考查空间直线和平面平行的判定以及线面垂直的性质,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
相关题目
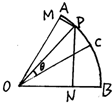 如图,扇形OAB的半径为2,圆心角为
如图,扇形OAB的半径为2,圆心角为