已知函数f(x)=|x+2|-|x-2|.试判断f(x)的奇偶性．题目和参考答案——青夏教育精英家教网—

题目内容

已知函数f（x）=|x+2|-|x-2|，试判断f（x）的奇偶性．

考点：函数奇偶性的判断

专题：函数的性质及应用

分析：首先求出定义域为R，关于原点对称，然后判断f（-x）与f（x）的关系．

解答： 解：f（x）的定义域为R，关于原点对称，
又f（-x）=|-x+2|-|-x-2|=|x-2|-|x+2|=-f（x），
∴f（x）=|x+2|-|x-2|是奇函数．

点评：本题考查了函数奇偶性的判定；①判断函数的定义域是否关于原点对称；②如果不对称是非奇非偶的函数；如果对称，再利用定义判断f（-x）与f（x）的关系．

练习册系列答案

相关题目

在△ABC中，a、b、c分别是角A、B、C的对边，A=60°，B＜C，b、c是方程x²-2

x+m=0的两个实根，△ABC的面积为

．
（1）求m的值；
（2）求△ABC的三边长．

已知一个二次函数y=f（x）的抛物线先向左平移2个单位长度，再向下平移2个单位长度，此时抛物线过点（-1，-1），对称轴为x=-2，且在x轴上截得的线段长为2

．
（1）求f（x）解析式；
（2）求函数y=f（x）的单调递减区间；
（3）在给出的直角坐标系中用“五点作图法”画出函数y=f（x）在[0，π]上的图象．
（要求列表、描点、连线）

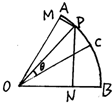如图，扇形OAB的半径为2，圆心角为

，∠AOB的平分线交弧AB于点C，P为弧AC上一点，PM⊥OA于M，PN⊥OB于N，若设∠POC=θ．
﹙Ⅰ﹚写出四边形OMPN的面积S关于θ的函数关系式及其定义域；
﹙Ⅱ﹚P点在何处时S最大？最大值是多少？

已知双曲线C₁：

13x2

13y2

=1，点A、B分别为双曲线C₁的左、右焦点，动点C在x轴上方．
（1）若点C的坐标为C（x₀，3）（x₀＞0）是双曲线的一条渐近线上的点，求以A、B为焦点且经过点C的椭圆的方程；
（2）若∠ACB=45°，求△ABC的外接圆的方程；
（3）若在给定直线y=x+t上任取一点P，从点P向（2）中圆引一条切线，切点为Q．问是否存在一个定点M，恒有|PM|=|PQ|？请说明理由．

已知函数f（x）的定义域A=（m+1，2m），B=[0，4]且A⊆B，则m的取值范围为

．

试题分类