题目内容
已知数列{an}的前n项和为Sn,记f(n)=2an+1Sn-n(2Sn+an+1),n∈N*
(1)若数列{an}是首项与公差均为1的等差数列,求f(2014);
(2)若a1=1,a2=2且数列{a2n-1},{a2n}均是公比为4的等比数列,求证:对任意正整数n,f(n)≥0.
(1)若数列{an}是首项与公差均为1的等差数列,求f(2014);
(2)若a1=1,a2=2且数列{a2n-1},{a2n}均是公比为4的等比数列,求证:对任意正整数n,f(n)≥0.
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(1)依题意,可求得an=n,an+1=n+1,Sn=
,于是可求得f(n)=0,从而可求f(2014);
(2)依题意,可求得an=2n-1,于是可求得f(n)=2an+1Sn-n(2Sn+an+1)=2n(2n+1-3n-2)+2n,对n分n=1与n≥2讨论,即可证得对任意正整数n,f(n)≥0.
| n(n+1) |
| 2 |
(2)依题意,可求得an=2n-1,于是可求得f(n)=2an+1Sn-n(2Sn+an+1)=2n(2n+1-3n-2)+2n,对n分n=1与n≥2讨论,即可证得对任意正整数n,f(n)≥0.
解答:
解:(1)∵数列{an}是首项与公差均为1的等差数列,
∴an=n,an+1=n+1,Sn=
,
∴f(n)=2an+1Sn-n(2Sn+an+1)
=2(n+1)×
-n[2×
+(n+1)]
=n(n+1)2-n(n+1)2=0,
∴f(2014)=0;
(2)由题意?n∈N*,a2n-1=1×4n-1=22n-2,
a2n=2×4n-1=22n-1,
∴an=2n-1,
∴an+1=2n,Sn=
=2n-1,
∴f(n)=2an+1Sn-n(2Sn+an+1)
=2n+1(2n-1)-n(2n+1-2+2n)
=2n(2n+1-3n-2)+2n,
当n=1时,f(1)=0;
当n≥2时,2n+1=4×(1+1)n-1≥4[1+(n-1)]=4n,
∴f(n)=2n(2n+1-3n-2)+2n≥2n(4n-3n-2)+2n=2n(n-2)+2n≥2n>0,
故对任意正整数n,f(n)>0.
∴an=n,an+1=n+1,Sn=
| n(n+1) |
| 2 |
∴f(n)=2an+1Sn-n(2Sn+an+1)
=2(n+1)×
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
=n(n+1)2-n(n+1)2=0,
∴f(2014)=0;
(2)由题意?n∈N*,a2n-1=1×4n-1=22n-2,
a2n=2×4n-1=22n-1,
∴an=2n-1,
∴an+1=2n,Sn=
| 1-2n |
| 1-2 |
∴f(n)=2an+1Sn-n(2Sn+an+1)
=2n+1(2n-1)-n(2n+1-2+2n)
=2n(2n+1-3n-2)+2n,
当n=1时,f(1)=0;
当n≥2时,2n+1=4×(1+1)n-1≥4[1+(n-1)]=4n,
∴f(n)=2n(2n+1-3n-2)+2n≥2n(4n-3n-2)+2n=2n(n-2)+2n≥2n>0,
故对任意正整数n,f(n)>0.
点评:本题考查数列的求和,着重考查等差数列与等比数列的通项公式与求和公式的综合应用,突出考查分类讨论思想与放缩法的应用,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知曲线C:x2+y2-2x+2y=0与直线L:y+2=k(x-2),则C与L的公共点( )
| A、有2个 | B、最多1个 |
| C、至少1个 | D、不存在 |
在区域D:(x-1)2+y2≤4内随机取一个点,则此点到点A(1,2)的距离大于2的概率是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如果直线ax+by=2与圆x2+y2=4相切,那么a+b的最大值为( )
| A、1 | ||||
B、
| ||||
| C、2 | ||||
D、
|
 如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.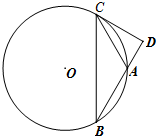 【几何证明选讲选做题】
【几何证明选讲选做题】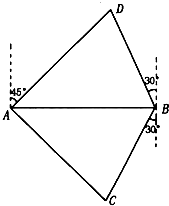 如图,A,B是海面上位于东西方向相距
如图,A,B是海面上位于东西方向相距