题目内容
设函数f(x)=sin2ωx+2
sinωx•cosωx-cos2ωx+λ,(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
,0),求函数f(x)在x∈[0,
]上的值域.
| 3 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
| π |
| 4 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:
分析:(1)利用二倍角的正弦与余弦可求得f(x)=2sin(2ωx-
)+λ,利用其图象关于直线x=π对称,可求得sin(2ωπ-
)=±1,继而得ω=
+
(k∈Z),于是可求得ω及函数f(x)的最小正周期;
(2)由y=f(x)的图象过点(
,0),可求得λ=-
,于是知f(x)=2sin(
x-
)-
,x∈[0,
]⇒
x-
∈[-
,
],利用正弦函数的性质可求得x∈[0,
]时函数f(x)的值域.
| π |
| 6 |
| π |
| 6 |
| k |
| 2 |
| 1 |
| 3 |
(2)由y=f(x)的图象过点(
| π |
| 4 |
| 2 |
| 5 |
| 3 |
| π |
| 6 |
| 2 |
| π |
| 2 |
| 5 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
解答:
解:(1)f(x)=sin2ωx-cos2ωx+2
sinωx•cosωx+λ
=-cos2ωx+
sin2ωx+λ
=2sin(2ωx-
)+λ,
由直线x=π是y=f(x)图象的一条对称轴,可得:
sin(2ωπ-
)=±1,
∴2ωπ-
=kπ+
(k∈Z),即ω=
+
(k∈Z).
又ω∈(
,1),k∈Z,
∴k=1,故ω=
.
∴f(x)的最小正周期是
.
(2)由y=f(x)的图象过点(
,0),得f(
)=0,
即λ=-2sin(
×
-
)=-2sin
=-
,
即λ=-
.
故f(x)=2sin(
x-
)-
,
∵x∈[0,
],
∴
x-
∈[-
,
],
∴-
≤sin(
x-
)≤1,
∴函数f(x)的值域为[-1-
,2-
].
| 3 |
=-cos2ωx+
| 3 |
=2sin(2ωx-
| π |
| 6 |
由直线x=π是y=f(x)图象的一条对称轴,可得:
sin(2ωπ-
| π |
| 6 |
∴2ωπ-
| π |
| 6 |
| π |
| 2 |
| k |
| 2 |
| 1 |
| 3 |
又ω∈(
| 1 |
| 2 |
∴k=1,故ω=
| 5 |
| 6 |
∴f(x)的最小正周期是
| 6π |
| 5 |
(2)由y=f(x)的图象过点(
| π |
| 4 |
| π |
| 4 |
即λ=-2sin(
| 5 |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
| 2 |
即λ=-
| 2 |
故f(x)=2sin(
| 5 |
| 3 |
| π |
| 6 |
| 2 |
∵x∈[0,
| π |
| 2 |
∴
| 5 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴-
| 1 |
| 2 |
| 5 |
| 3 |
| π |
| 6 |
∴函数f(x)的值域为[-1-
| 2 |
| 2 |
点评:本题考查三角函数中的恒等变换应用,着重考查正弦函数的周期性、对称性与单调性,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果直线ax+by=2与圆x2+y2=4相切,那么a+b的最大值为( )
| A、1 | ||||
B、
| ||||
| C、2 | ||||
D、
|
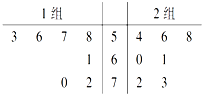 如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为
如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
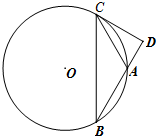 【几何证明选讲选做题】
【几何证明选讲选做题】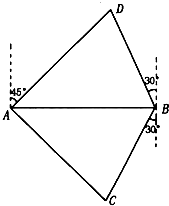 如图,A,B是海面上位于东西方向相距
如图,A,B是海面上位于东西方向相距