题目内容
连掷两次骰子得到的点数分别为m和n,若记向量
=(m,n)与向量
=(1,-2)的夹角为θ,则θ为锐角的概率是( )
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:掷两次骰子分别得到的点数m,n,组成的向量(m,n)个数为36个,只需列举出满足条件向量
=(m,n)与向量
=(1,-2)的夹角为θ的基本事件即可求出概率.
| a |
| b |
解答:
解:连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种
由于向量
=(m,n)与向量
=(1,-2)的夹角为θ,∴(m,n)•(1,-2)>0,且-2m≠n,
即m>2n,满足题意的情况如下:
当m=3时,n=1;
当m=4时,n=1;
当m=5时,n=1,2;
当m=6时,n=1,2,共有6种,
故所求事件的概率为:
=
.
故选B.
由于向量
| a |
| b |
即m>2n,满足题意的情况如下:
当m=3时,n=1;
当m=4时,n=1;
当m=5时,n=1,2;
当m=6时,n=1,2,共有6种,
故所求事件的概率为:
| 6 |
| 36 |
| 1 |
| 6 |
故选B.
点评:本题考查概率的计算,考查向量知识的运用,确定满足条件向量
=(m,n)与向量
=(1,-2)的夹角为θ的基本事件是关键.
| a |
| b |

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的体积是( )
A、
| ||||
B、
| ||||
C、2S
| ||||
D、S
|
若函数f(x)=(ax+1)(x-a)为偶函数,且函数y=f(x)在x∈(0,+∞)上单调递增,则实数a的值为( )
| A、±1 | B、-1 | C、1 | D、0 |
 如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.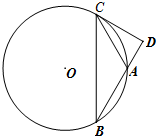 【几何证明选讲选做题】
【几何证明选讲选做题】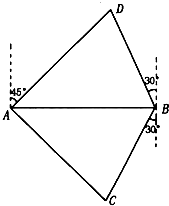 如图,A,B是海面上位于东西方向相距
如图,A,B是海面上位于东西方向相距