题目内容
已知x,y∈Z,n∈N*,设f(n)是不等式组
表示的平面区域内可行解的个数,则f(2)= .
|
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:根据不等式组解表示平面区域,即可求出f(2)的个数.
解答:
解:当n=2时,不等式组对应为
,
当x=1时,不等式组等价为
,此时0≤y≤1,即y=0或y=1,此时对应整数点为(1,0),(1,1).
当x=2时,不等式组等价为
,此时y=0,此时对应整数点为(2,0).
当x≥3时,不等式组等价为
,此时不等式无解.
故f(2)=3,
故答案为:3
|
当x=1时,不等式组等价为
|
当x=2时,不等式组等价为
|
当x≥3时,不等式组等价为
|
故f(2)=3,
故答案为:3
点评:本题主要考查二元二次不等式组的应用,分别讨论x的取值即可,比较基础.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
如果直线ax+by=2与圆x2+y2=4相切,那么a+b的最大值为( )
| A、1 | ||||
B、
| ||||
| C、2 | ||||
D、
|
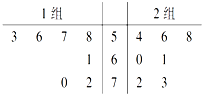 如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为
如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
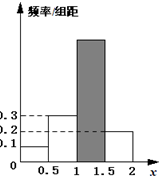 如图所示的频率分布直方图,其中阴影部分的小长方形的高度是( )
如图所示的频率分布直方图,其中阴影部分的小长方形的高度是( )| A、0.4 | B、0.8 |
| C、1.4 | D、1.6 |
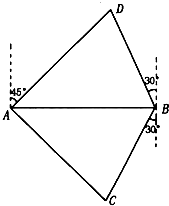 如图,A,B是海面上位于东西方向相距
如图,A,B是海面上位于东西方向相距 如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )
如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )



 已知几何体A-BCDE的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则该几何体的体积V的大小为
已知几何体A-BCDE的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则该几何体的体积V的大小为