题目内容

已知函数f（x）=ax2+bx+c，且f（x）＞0的解集为（-2，1），则函数y=f（-x）的图象是（　　）
A、
B、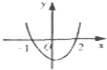
C、
D、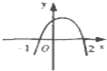
考点：函数的图象
专题：函数的性质及应用
分析：根据f（x）＞0的解集为（-2，1），确定对应方程的根，然后根据函数y=f（-x）与y=f（x）的关系即可确定答案．
解答： 解：∵f（x）＞0的解集为（-2，1），
∴a＜0，且-2，1是方程f（x）=ax2+bx+c=0的两个根，
令t=-x，
则x=-t，即y=f（-x）的两个零点为2，-1，且抛物线开口向下，
∴D图象正确．
故选：D．
点评：本题主要考查函数图象的识别和判断，利用二次函数的图象和性质是解决本题的关键．
练习册系列答案
相关题目
已知等比数列{an}的公比q=
1
2
，其前4项和S4=60，则a2等于（　　）
A、8B、12C、16D、20
已知函数f（x），当x，y∈R时，恒有f（x+y）=f（x）+f（y）．当x＞0时，f（x）＞0
（1）求证：f（x）是奇函数；
（2）若f(1)=
1
2
，试求f（x）在区间[-2，6]上的最值；
（3）是否存在m，使f(2(log2x)2-4)+f(4m-2(log2x))＞0对于任意x∈[1，2]恒成立？若存在，求出实数m的取值范围；若不存在，说明理由．
设x∈R，向量
a
=(x，1)，
b
=(1，-2)，若|
a
+
b
|=|
a
-
b
|，则x=
 
．
直线x+ay+2=0与圆锥曲线x2+2y2=2有两个交点，则实数a的取值范围为（　　）
A、(-∞，-
2
)∪(
2
，+∞)
B、（-
2
，
2
）
C、（-∞，-2）∪（2，+∞）
D、（-2，2）
已知函数f(x)=
3-x2(x＞0)
3(x=0)
2x+2(x＜0)
，
（1）画出函数f（x）图象；
（2）若f(x)＞
5
2
，求x的取值范围．
求满足下列条件的实数x的范围：
（1）2x＞8；             
（2）3x＜
1
27
；                 
（3）（
1
2
）x＞
2
．
设a、b是非负实数，且a2+b2=4，则
ab
a+b+2
（　　）
A、有最大值
2
+1
B、有最小值
2
+1
C、有最大值
2
-1
D、有最小值
2
-1
已知函数f（x）满足f(x+
1
2
)=log
1
2
(x2-
9
4
)，且函数g(x)=log
1
2
(2x-2)
（1）求函数f（x）的表达式及定义域；
（2）若f（x）＞g（x），求x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网