题目内容
已知函数f(x)=
,
(1)画出函数f(x)图象;
(2)若f(x)>
,求x的取值范围.
|
(1)画出函数f(x)图象;
(2)若f(x)>
| 5 |
| 2 |
考点:其他不等式的解法,分段函数的解析式求法及其图象的作法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)根据分段函数的解析式,分段画出图象即可;
(2)根据每一段的解析式分别进行讨论,列出不等关系,求解即可得到答案.
(2)根据每一段的解析式分别进行讨论,列出不等关系,求解即可得到答案.
解答:
解:(1)∵函数f(x)=
,
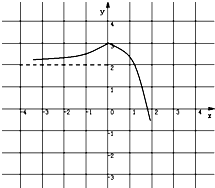
故作出f(x)的图象如图所示;
 (2)∵函数f(x)=
(2)∵函数f(x)=
,
①当x>0时,f(x)=3-x2,
则f(x)>
,
即3-x2>
,
整理可得x2<
,
解得-
<x<
,
又∵x>0,
∴x的取值范围为(0,
);
②当x=0时,f(x)=3>
,
∴x=0符合题意;
③当x<0时,f(x)=2x+2,
则f(x)>
,即2x+2>
,
整理可得2x>
,解得x>-1,
又∵x<0,
∴x的取值范围为(-1,0).
综合①②③可得,x的取值范围为(-1,
).
|
故作出f(x)的图象如图所示;
 (2)∵函数f(x)=
(2)∵函数f(x)=
|
①当x>0时,f(x)=3-x2,
则f(x)>
| 5 |
| 2 |
即3-x2>
| 5 |
| 2 |
整理可得x2<
| 1 |
| 2 |
解得-
| ||
| 2 |
| ||
| 2 |
又∵x>0,
∴x的取值范围为(0,
| ||
| 2 |
②当x=0时,f(x)=3>
| 5 |
| 2 |
∴x=0符合题意;
③当x<0时,f(x)=2x+2,
则f(x)>
| 5 |
| 2 |
| 5 |
| 2 |
整理可得2x>
| 1 |
| 2 |
又∵x<0,
∴x的取值范围为(-1,0).
综合①②③可得,x的取值范围为(-1,
| ||
| 2 |
点评:本题考查了分段函数的图象的画法,分段函数不等式的解法.对于分段函数的问题,一般选用分类讨论和数形结合的思想方法进行求解,根据分段函数的图象很容易得到相关的性质,若选用分类讨论的方法,则关键是讨论需用哪段解析式进行求解.属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知函数f(x)=
,则f(-2)=( )
|
| A、0 | B、1 | C、-2 | D、-1 |