题目内容
12.函数y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$的最小值为$\frac{3\sqrt{2}}{2}$.分析 令$\sqrt{{x}^{2}+2}$=t$≥\sqrt{2}$,可得:y=$t+\frac{1}{t}$=g(t),利用导数研究函数的单调性即可得出.
解答 解:令$\sqrt{{x}^{2}+2}$=t$≥\sqrt{2}$,
∴y=$t+\frac{1}{t}$=g(t),
g′(t)=1-$\frac{1}{{t}^{2}}$=$\frac{{t}^{2}-1}{{t}^{2}}$>0,
∴函数g(t)在$[\sqrt{2},+∞)$上单调递增,
∴g(t)的最小值为:$\sqrt{2}+\frac{1}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知$\overrightarrow a=(cosx,-2),\overrightarrow b=(sinx,1)$且$\overrightarrow a$∥$\overrightarrow b$,则sin2x=( )
| A. | $-\frac{4}{5}$ | B. | -3 | C. | 3 | D. | $\frac{4}{5}$ |
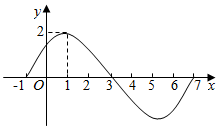 下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).