题目内容
10.反比例函数y=$\frac{k}{x}$(k≠0)的图象经过(-2,5)和($\sqrt{2}$,n),求(1)n的值;
(2)判断点B(4$\sqrt{2}$,-$\sqrt{2}$)是否在这个函数图象上,并说明理由.
分析 (1)利用待定系数法求得该反比例函数y=$\frac{k}{x}$(k≠0)的解析式;然后将x=2代入该反比例函数解析式求n值即可;
(2)根据反比例函数图象上点的坐标特征,将点B的坐标代入该反比例函数解析式进行验证即可.
解答 解:(1)把x=-2,y=5代入y=$\frac{k}{x}$得k=-10,
∴y=$-\frac{10}{x}$,
当x=$\sqrt{2}$,时,y=-5$\sqrt{2}$;
(2)将x=4$\sqrt{2}$,代入y=$-\frac{10}{x}$得:y=$-\frac{5}{4}\sqrt{2}$≠-$\sqrt{2}$,
∴点B,不在函数图象上.
点评 本题考查了待定系数法求反比例函数解析式、反比例函数图象上点的坐标特征.反比例函数y=$\frac{k}{x}$(k≠0)的图象上所有点的坐标均满足该函数的关系式,属于基础题.

练习册系列答案
相关题目
1.如图,该程序运行后输出的结果为( )


| A. | 7 | B. | 11 | C. | 25 | D. | 36 |
18.若$\overrightarrow{a}$=(2,3,m),$\overrightarrow{b}$=(2n,6,8)且$\overrightarrow{a}$,$\overrightarrow{b}$为共线向量,则m+n的值为( )
| A. | 7 | B. | $\frac{5}{2}$ | C. | 6 | D. | 8 |
5.要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如表所示:
今需要三种规格的成品分别为12、15、27块,用数学关系式和图形表示上述要求.
| 规格类型 钢板类型 | A | B | C |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 2 | 1 | 3 |
15.一个几何体的三视图如图,则该几何体的体积为( )
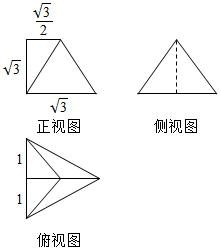

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |