题目内容
20.下列四个结论中,正确的有( )(填所有正确结论的序号).①若A是B的必要不充分条件,则非B也是非A的必要不充分条件;
②“$\left\{\begin{array}{l}{a>0}\\{△={b}^{2}-4ac}≤0\end{array}\right.$”是“一元二次不等式ax2+bx+c≥0的解集为R”的充要条件
③“x≠1”是“x2≠1”的充分不必要条件;
④“x≠0”是“x+|x|>0”的必要不充分条件.
| A. | ①② | B. | ②③ | C. | ①②④ | D. | ②③④ |
分析 ①根据逆否命题的等价性以及充分条件和必要条件的定义进行判断.
②根据不等式恒成立的等价条件进行判断.
③根据充分条件和必要条件的定义进行判断.
④根据充分条件和必要条件的定义进行判断.
解答 解:①若A是B的必要不充分条件,则根据逆否命题的等价性知,非B也是非A的必要不充分条件;故①正确,
②一元二次不等式ax2+bx+c≥0的解集为R,则满足$\left\{\begin{array}{l}{a>0}\\{△={b}^{2}-4ac≤0}\end{array}\right.$,
则$\left\{\begin{array}{l}{a>0}\\{△={b}^{2}-4ac≤0}\end{array}\right.$是“一元二次不等式ax2+bx+c≥0的解集为R”的充要条件;故②正确,
③当x=-1时,满足x≠1,但x2≠1不成立,即充分性不成立,即“x≠1”是“x2≠1”即”的充分不必要条件错误,故③错误;
④由x+|x|>0得|x|>-x,则x>0,此时x≠0成立,即必要性成立,
当x<0时,满足“x≠0”,但x+|x|=0,则x+|x|>0不成立,即充分性不成立,即④“x≠0”是“x+|x|>0”的必要不充分条件错误,故④错误,
故正确的是①②,
故选:A
点评 本题主要考查命题的真假判断,涉及充分条件和必要条件的判断,根据不等式的关系以及充分条件和必要条件的定义是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.当点P(3,2)到直线mx-y+1-2m=0的距离最大值时,m的值为( )
| A. | $\sqrt{2}$ | B. | 0 | C. | -1 | D. | 1 |
12.已知a∈($\frac{π}{2}$,π),sinα+cosα=$\frac{\sqrt{2}}{2}$,则$\frac{cos2α}{cos(α-\frac{π}{4})}$的值为( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
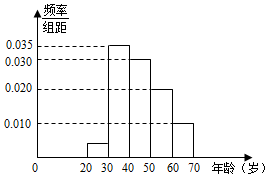 某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.
某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.