题目内容

18．若$\overrightarrow{a}$=（2，3，m），$\overrightarrow{b}$=（2n，6，8）且$\overrightarrow{a}$，$\overrightarrow{b}$为共线向量，则m+n的值为（　　）
A．7B．$\frac{5}{2}$C．6D．8

分析 根据两向量共线的坐标表示，列出方程求出m、n的值即可．

解答 解：∵$\overrightarrow{a}$=（2，3，m），$\overrightarrow{b}$=（2n，6，8），且$\overrightarrow{a}$，$\overrightarrow{b}$为共线向量，
∴$\frac{2}{2n}$=$\frac{3}{6}$=$\frac{m}{8}$，
解得m=4，n=2；
∴m+n=6．
故选：C．

点评 本题考查了两向量共线的坐标表示与应用问题，是基础题目．

练习册系列答案
相关题目
8．某班主任在其工作手册中，对该班每个学生用十二项能力特征加以描述．每名学生的第i（i=1，2，…，12）项能力特征用xi表示，${x_i}=\left\{{\begin{array}{l}{0，\;\;如果某学生不具有第i项能力特征}\\{1，\;如果某学生具有第i项能力特征}\end{array}}\right.$，若学生A，B的十二项能力特征分别记为A=（a1，a2，…，a12），B=（b1，b2，…，b12），则A，B两名学生的不同能力特征项数为$\sum_{i=1}^{12}{|{a_i}-{b_i}|}$（用ai，bi表示）．如果两个同学不同能力特征项数不少于7，那么就说这两个同学的综合能力差异较大．若该班有3名学生两两综合能力差异较大，则这3名学生两两不同能力特征项数总和的最小值为22．
9．为配合上海迪斯尼游园工作，某单位设计人数的数学模型（n∈N+）：以f（n）=$\left\{\begin{array}{l}{200n+2000，n∈[1，8]}\\{360•{3}^{\frac{n-8}{12}}+3000，n∈[9，32]}\\{32400-720n，n∈[33，45]}\end{array}\right.$表示第n时进入人数，以g（n）=$\left\{\begin{array}{l}{0，n[1，18]}\\{500n-9000，n∈[19，32]}\\{8800，n∈[33，45]}\end{array}\right.$表示第n个时刻离开园区的人数；设定以15分钟为一个计算单位，上午9点15分作为第1个计算人数单位，即n=1：9点30分作为第2个计算单位，即n=2；依此类推，把一天内从上午9点到晚上8点15分分成45个计算单位：（最后结果四舍五入，精确到整数）．
（1）试计算当天14点到15点这一个小时内，进入园区的游客人数f（21）+f（22）+f（23）+f（24）、离开园区的游客人数g（21）+g（22）+g（23）+g（24）各为多少？
（2）假设当日园区游客人数达到或超过8万时，园区将采取限流措施，该单位借助该数学模型知晓当天16点（即n=28）时，园区总人数会达到最高，请问当日是否要采取限流措施？说明理由．
6．在△ABC中，已知a=3，b=4，c=$\sqrt{37}$，则△ABC的面积是3$\sqrt{3}$．
13．由方程|z|2-8|z|+15=0所确定的复数在复平面内对应点的轨迹是以原点为圆心，以3和5为半径的两个圆．
3．若执行如图所示的程序框图，输入x1=1，x2=2，x3=3，$\overline{x}$=2，则输出的数S等于（　　）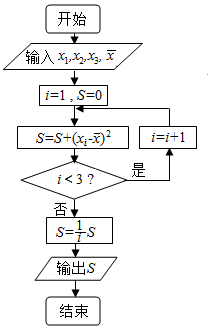
A．$\frac{2}{3}$B．1C．$\frac{1}{3}$D．$\frac{1}{2}$
10．反比例函数y=$\frac{k}{x}$（k≠0）的图象经过（-2，5）和（$\sqrt{2}$，n），
求（1）n的值；
（2）判断点B（4$\sqrt{2}$，-$\sqrt{2}$）是否在这个函数图象上，并说明理由．
7．已知函数f（x）=$\left\{\begin{array}{l}{|lo{g}_{3}x|，0＜x＜3}\\{sin（\frac{π}{2}x-π），3≤x≤7}\end{array}\right.$，若存在实数a，b，c，d，满足f（a）=f（b）=f（c）=f（d），其中0＜a＜b＜c＜d，则a+b+c+d的取值范围是（12，$\frac{40}{3}$）．
8．△ABC中，b-a=c-b=1，且C=2A，则cosC=$\frac{1}{8}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网