题目内容

函数f（x）=sin（2x-
π
6
）的一条对称轴方程是（　　）
A、x=
π
12
B、x=
π
6
C、x=
5π
12
D、x=
π
3
考点：正弦函数的对称性
专题：三角函数的图像与性质
分析：由条件利用正弦函数的图象的对称性求得f（x）=sin（2x-
π
6
）的一条对称轴方程．
解答： 解：对于函数f（x）=sin（2x-
π
6
），令2x-
π
6
=kπ+
π
2
，k∈z，求得x=
kπ
2
+
π
3
，k∈z，
可得函数的图象的对称轴方程为x=
kπ
2
+
π
3
，k∈z，
结合所给的选项，
故选：D．
点评：本题主要考查正弦函数的图象的对称性，属于基础题．
练习册系列答案
相关题目
设二次函数y=f（x）的最小值为4，且f（0）=f（2）=6，求f（x）的解析式．
因式分解：y（y+1）（x2+1）+x（2y2+2y+1）．
已知实数序列x0，x1，x2，…，xn…的构成规律由递推关系给出：x0=5，xn=xn-1+
1
xn-1
（n=1，2，3…）．求证：45＜x1000＜45.1．
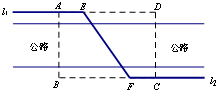如图，某自来水公司要在公路两侧铺设水管，公路为东西方向，在路北侧沿直线铺设线路l1，在路南侧沿直线铺设线路l2，现要在矩形区域ABCD内沿直线将l1与l2接通．已知AB=60m，BC=80m，公路两侧铺设水管的费用为每米1万元，穿过公路的EF部分铺设水管的费用为每米2万元，设∠EFB=
π
2
-α，矩形区域内的铺设水管的总费用为W．
（1）求W关于α的函数关系式；
（2）求W的最小值及相应的角α．
若一个几何体的主视图和侧视图都是等腰三角形，则这个几何体可能是（　　）
A、圆柱B、圆锥C、球体D、圆台
设函数f（1-x）=x，则f（x）的表达式为
 
．
若动直线x=a与函数f（x）=
3
sin（x+
π
6
）与g（x）=cos（x+
π
6
）的图象分别交于M、N两点，则|MN|的最大值为
 
．
在△ABC中，B=45°，A=75°，c=1，则最短边的边长为（　　）
A、
6
2
B、1
C、
3
2
+
6
12
D、
6
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网