题目内容
若动直线x=a与函数f（x）=
sin（x+
）与g（x）=cos（x+
）的图象分别交于M、N两点，则|MN|的最大值为 ．
| 3 |
| π |
| 6 |
| π |
| 6 |
考点：正弦函数的图象,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：根据三角函数的图象和性质，即可得到结论．
解答：
解：当x=a时，|MN|=|f（a）-g（a）|=|
sin（a+
）-cos（a+
）=|2sin（a+
-
）|=2|sina|，
∴当|sina|=1时，|MN|取得最大值2，
故答案为：2．
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴当|sina|=1时，|MN|取得最大值2，
故答案为：2．
点评：本题主要考查函数最值的求解，根据辅助角公式以及三角函数的图象和性质是解决本题的关键．
练习册系列答案
相关题目
函数f（x）=sin（2x-
）的一条对称轴方程是（ ）
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
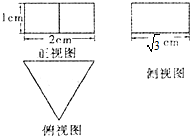某个几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的表面积是（ ）A、
| ||
B、6+
| ||
C、6+2
| ||
D、6+3
|