题目内容

解方程：|20-10k|=10
k2+1
．
考点：函数的零点与方程根的关系,有理数指数幂的化简求值,函数的零点
专题：函数的性质及应用
分析：直接利用平方化简求解即可．
解答： 解：|20-10k|=10
k2+1
．
可得（2-k）2=k2+1
4-4k+k2=k2+1．
解得k=
3
4
．
方程的解：
3
4
．
点评：本题考查方程的解的求法，函数的零点，考查计算能力．
练习册系列答案
相关题目
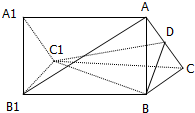如图，已知A1B1C1-ABC是正三棱柱（底面为正三角形，且侧棱垂直底面），D是AC的中点．求证：AB1∥平面DBC1．
下列命题
①函数y=sin2x的单调增区间是[
3π
4
+kπ，
5π
4
+kπ]，（k∈Z）；
②函数y=tanx在（0，π）内是增函数；
③函数y=|cos2x|的最小正周期是π；
④函数y=sin（
5π
2
+x）是偶函数；
其中正确的是（　　）
A、①②B、②③C、①③D、①④
给出下列命题：
①若f′（x0）=0，则函数f（x）在x=x0处有极值；
②m＞0是方程
x2
m
+
y2
4
=1表示椭圆的充要条件；
③若f（x）=（x2-8）ex，则f（x）的单调递减区间为（-4，2）；
④双曲线
x2
a2
-
y2
b2
=1的离心率为e1，双曲线
x2
b2
-
y2
a2
=1的离心率为e2，则e1+e2的最小值为2
2

其中为真命题的序号是
 
．
解不等式：
（1）log 
1
3
x≥1；
（2）a2x+1＜a4-x．
已知lgx=-2，则x=
 
．
已知直线l的倾斜角为
3π
4
，直线l1经过点A（3，2）B（a，-1），且与l垂直，直线l2：2x+by+1=0与直线l1平行，则a+b=
 
．
在△ABC中如果∠B=
π
3
，b2=ac，则△ABC为
 
三角形．
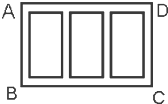如图，某广场要划定一矩形区域ABCD，并在该区域内开辟出三块形状大小相同的小矩形绿化区，这三块绿化区四周和绿化区之间均设有1米宽的走道，已知三块绿化区的总面积为200平方米，求该矩形区域ABCD占地面积的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网