题目内容
解不等式:
(1)log
x≥1;
(2)a2x+1<a4-x.
(1)log
| 1 |
| 3 |
(2)a2x+1<a4-x.
考点:指、对数不等式的解法
专题:不等式的解法及应用
分析:(1)直接利用对数的性质,化简log
x≥1,求解即可;
(2)通过a范围讨论,结合指数函数的单调性求解a2x+1<a4-x.
| 1 |
| 3 |
(2)通过a范围讨论,结合指数函数的单调性求解a2x+1<a4-x.
解答:
解:(1)log
x>1=log
(
)
∴0<x<
即解集为{x|0<x<
}-----(7分)
(2)a2x+1<a4-x
当a>1时,有2x+1<4-x,∴{x|x<1}---------(10分)
当0<a<1时,有2x+1>4-x,∴{x|x>1}----------(14分)
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴0<x<
| 1 |
| 3 |
| 1 |
| 3 |
(2)a2x+1<a4-x
当a>1时,有2x+1<4-x,∴{x|x<1}---------(10分)
当0<a<1时,有2x+1>4-x,∴{x|x>1}----------(14分)
点评:本题考查指数不等式以及对数不等式的解法,考查分类讨论思想的应用,考查计算能力.

练习册系列答案
相关题目
下列有关命题的叙述错误的是( )
| A、对于命题p:?x0∈R,x02+x0+1<0,则¬p为:?x∈R,x2+x+1≥0 |
| B、若p∧q为假命题,则p,q均为假命题 |
| C、命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
| D、x2-5x+6=0是x=2的必要不充分条件 |
指数函数①f(x)=mx;②g(x)=nx;满足不等式m>n>1,则它们的图象是( )


| A、A、 | B、B、 | C、C、 | D、D、 |
等比数列{an}的前n项和为Sn=3n-1,则a12+a22+…+an2=( )
A、
| ||
| B、(3n-1) | ||
C、
| ||
| D、(9n-1) |
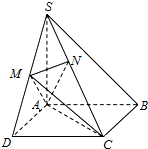 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.