题目内容
11.证明:(1)求证:sinθ(1+tanθ)+cosθ•(1+$\frac{1}{tanθ}$)=$\frac{1}{sinθ}$+$\frac{1}{cosθ}$.$(2)证明:\frac{tanx×sinx}{tanx-sinx}=\frac{tanx+sinx}{tanx×sinx}$.分析 (1)左边=sinθ(1+$\frac{sinθ}{cosθ}$)+cosθ•(1+$\frac{cosθ}{sinθ}$)=sinθ+$\frac{si{n}^{2}θ}{cosθ}$+cosθ+$\frac{co{s}^{2}θ}{sinθ}$,重新组合利用平方关系即可得出.
(2)由tan2x-sin2x=tan2x-(tanxcosx)2=tan2x(1-cos2x)=tan2xsin2x,进而证明结论.
解答 证明:(1)证明:左边=sinθ(1+$\frac{sinθ}{cosθ}$)+cosθ•(1+$\frac{cosθ}{sinθ}$)
=sinθ+$\frac{si{n}^{2}θ}{cosθ}$+cosθ+$\frac{co{s}^{2}θ}{sinθ}$=(sinθ+$\frac{co{s}^{2}θ}{sinθ}$)+($\frac{si{n}^{2}θ}{cosθ}$+cosθ)=$\frac{si{n}^{2}θ+co{s}^{2}θ}{sinθ}$+$\frac{si{n}^{2}θ+co{s}^{2}θ}{cosθ}$=$\frac{1}{sinθ}$+$\frac{1}{cosθ}$=右边,
∴原式成立.
(2)∵tan2x-sin2x=tan2x-(tanxcosx)2=tan2x(1-cos2x)=tan2xsin2x,
∴$\frac{tanxsinx}{tanx-sinx}$=$\frac{tanx+sinx}{tanxsinx}$.
点评 本题考查了同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
2.在正方体ABCD-A1B1C1D1中,设点P在线段CC1上,直线DP与平面A1BD所成的角为α,则sinα的取值范围是( )
| A. | [$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{2}}{3}$] | B. | [$\frac{\sqrt{6}}{3}$,$\frac{2\sqrt{2}}{3}$] | C. | [$\frac{2\sqrt{2}}{3}$,1] | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$] |
19.如图所示,在?ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△CDF为( )
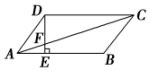

| A. | 54 cm2 | B. | 24 cm2 | C. | 18 cm2 | D. | 12 cm2 |
1.已知函数f(x)=ax-ln x,若f(x)>1在区间(1,+∞)内恒成立,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
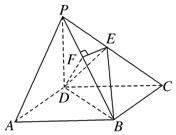 如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.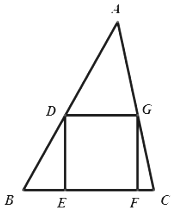 如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,