题目内容
6.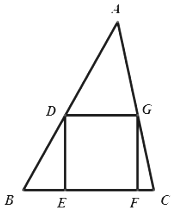 如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,DG∥BC,求正方形DEFG面积的最大值.
分析 过点A作AN⊥BC交DG于点M,交BC于点N,设AN=h,DE=x=MN=DG,根据DG∥BC,再由△ADG∽△ABC即可求出x的表达式,由根的判别式可得${x^2}≤\frac{1}{2}$,即可求正方形DEFG面积的最大值.
解答 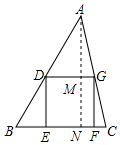 解:过点A作AN⊥BC交DG于点M,交BC于点N,
解:过点A作AN⊥BC交DG于点M,交BC于点N,
设AN=h,DE=x=MN=DG,
∴$\frac{1}{2}$BC•h=1,
∵DG∥BC,
∴△ADG∽△ABC,故$\frac{DG}{BC}=\frac{AM}{AN}$,即$\frac{x}{\frac{2}{h}}=\frac{h-x}{h}$,
∴h2x-2h+2x=0,
由根的判别式可得${x^2}≤\frac{1}{2}$,即正方形最大面积为$\frac{1}{2}$.
点评 本题考查的是相似三角形的判定与性质,根据题意构造出直角三角形是解答此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
8.设函数$f(x)=2x+\frac{1}{x}-1(x>0)$,则f(x)( )
| A. | 有最小值 | B. | 有最大值 | C. | 是增函数 | D. | 是减函数 |
9.设函数f(0)x=sinx,定义f(1)x=f′[f(0)(x)],f(2)(x)=f′[f(1)(x)],…,f(n)(x)=f′[f(n-1)(x)],则f(1)(150)+f(2)(150)+f(3)(150)+…+f(2017)(150)的值是( )
| A. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | 0 | D. | 1 |
1.在△ABC中,∠BAC=90°,AD是BC边上的高,则相似三角形共有( )
| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
18.设某校新、老校区之间开车单程所需时间为T,T只与道路畅通状况有关,对其容量为200的样本进行统计,结果如下:
(1)求T的分布列与数学期望ET;
(2)唐教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求唐教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
| T(分钟) | 25 | 30 | 35 | 40 |
| 频数(次) | 40 | 60 | 80 | 20 |
(2)唐教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求唐教授从离开老校区到返回老校区共用时间不超过120分钟的概率.