题目内容
若集合A={x|x≥0}，且A∩B=B，则集合B可能是（ ）
| A、{1，2} |
| B、{x|x≤1} |
| C、{-1，0，1} |
| D、R |
考点：交集及其运算
专题：计算题,集合
分析：由集合A={x|x≥0}，且A∩B=B，得B⊆A，由此能求出结果．
解答：
解：∵集合A={x|x≥0}，且A∩B=B，
∴B⊆A，
观察备选答案中的4个选项，
只有{1，2}⊆A．
故选：A．
∴B⊆A，
观察备选答案中的4个选项，
只有{1，2}⊆A．
故选：A．
点评：本题考查交集性质的应用，是基础题，解题时要认真审题．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
下列函数中，既是偶函数又在（0，+∞）上单调递增的是（ ）
| A、y=ln|x| |
| B、y=-x2 |
| C、y=ex |
| D、y=cosx |
已知数列{an}中，a1=1，且
=
+3（n∈N*），则a2015=（ ）
| 1 |
| an+1 |
| 1 |
| an |
| A、6042 | ||
| B、6048 | ||
C、
| ||
D、
|
将4个不同颜色的小球全部放入不同标号的3个盒子中，可以有一个或者多个盒子空着的放法种数为（ ）
| A、96 | B、36 | C、64 | D、81 |
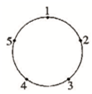如图，圆周上按顺时针方向标有1，2，3，4，5五个点，一只青蛙按顺时针方向绕圆从一个点跳到另一点；若停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次可以跳两个点，该青蛙从5这点跳起，跳2008次后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
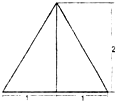一个三棱锥的侧棱长都相等，底面是正三角形，其正（主）视图如右图所示．该三棱锥侧面积和体积分别是（ ）A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、8，
|
函数y=f（x）为偶函数，且[0，+∞）上单调递减，则y=f（2-x2）的一个单调递增区间为（ ）
| A、（-∞，0] | ||
| B、[0，+∞） | ||
C、[0，
| ||
D、[
|