题目内容
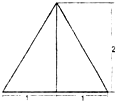 一个三棱锥的侧棱长都相等,底面是正三角形,其正(主)视图如右图所示.该三棱锥侧面积和体积分别是( )
一个三棱锥的侧棱长都相等,底面是正三角形,其正(主)视图如右图所示.该三棱锥侧面积和体积分别是( )A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、8,
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由题意得三棱锥S-ABC中,SA=SB=SC,高SD=2,△ABC是边长为2的等边三角形,由此能求出三棱锥侧面积和体积.
解答:
解:如图,由题意得三棱锥S-ABC中,
SA=SB=SC,
高SD=2,△ABC是边长为2的等边三角形,
∴S△ABC=
×2×2×sin60°=
,
∴该三棱锥的体积V=
×
×2=
.
∵SD⊥平面ABC,∴D是△ABC重心,
∴DE=
AE=
,SE⊥BC,
SE=
=
,
∴S△SAB=S△SAC=S△SBC=
×2×
=
,
∴该三棱锥侧面积S=
.
故选:A.

SA=SB=SC,
高SD=2,△ABC是边长为2的等边三角形,
∴S△ABC=
| 1 |
| 2 |
| 3 |
∴该三棱锥的体积V=
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
∵SD⊥平面ABC,∴D是△ABC重心,
∴DE=
| 1 |
| 3 |
| ||
| 3 |
SE=
22+(
|
| ||
| 3 |
∴S△SAB=S△SAC=S△SBC=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
∴该三棱锥侧面积S=
| 39 |
故选:A.
点评:本题考查三棱锥侧面积和体积的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)的定义域为A,且满足任意x∈A恒有 f(x)+f(2-x)=2的函数可以是( )
A、f(x)=log2(x+
| ||
| B、f(x)=(x-2)3+1 | ||
C、f(x)=
| ||
| D、f(x)=(x-1)2 |
若集合A={x|x≥0},且A∩B=B,则集合B可能是( )
| A、{1,2} |
| B、{x|x≤1} |
| C、{-1,0,1} |
| D、R |
若直线y=
x+2绕其与y轴的交点逆时针旋转
,则此时直线在x轴上的截距是( )
| 2 |
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
已知直线l:x+my+4=0,若曲线x2+y2+2x-6y+1=0上存在两点P、Q关于直线l对称,则m的值为( )
| A、2 | B、-2 | C、1 | D、-1 |
下列函数中,既是奇函数又是增函数的为( )
| A、y=x+1 | ||
| B、y=-x3 | ||
C、y=
| ||
| D、y=x|x| |
已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求P(ξ=4)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )
A、
| ||
| B、a km | ||
C、
| ||
| D、2a km |
定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上单调递增,设a=f(3),b=f(
),c=f(-2),则a,b,c大小关系是( )
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、c>b>a y |