题目内容
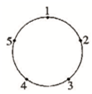如图，圆周上按顺时针方向标有1，2，3，4，5五个点，一只青蛙按顺时针方向绕圆从一个点跳到另一点；若停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次可以跳两个点，该青蛙从5这点跳起，跳2008次后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
考点：归纳推理
专题：计算题,推理和证明
分析：利用所给的规则把问题转化为一个周期数列问题即可解决．
解答：
解：如图所示：
将青蛙的起跳点和落脚点依次组成一个数列{an}，根据规则“起跳点为奇数，则落点与起跳点相邻；若起跳点为偶数，则落点与起跳相隔一个点”．并且该青蛙从5这点开始起跳，于是可得a1=5，a2=1，a3=2，a4=4，a5=1，…，因此从n=2开始有an+3=an，
要求的是经过2008次跳动，故要求的是a2009=a2+669×3=a2=1．
故最终停在的点为1．
故选A．
将青蛙的起跳点和落脚点依次组成一个数列{an}，根据规则“起跳点为奇数，则落点与起跳点相邻；若起跳点为偶数，则落点与起跳相隔一个点”．并且该青蛙从5这点开始起跳，于是可得a1=5，a2=1，a3=2，a4=4，a5=1，…，因此从n=2开始有an+3=an，
要求的是经过2008次跳动，故要求的是a2009=a2+669×3=a2=1．
故最终停在的点为1．
故选A．
点评：正确理解所给的规则及把要求问题转化为一个周期数列问题是解题的关键．
练习册系列答案
相关题目
已知f（x）=x3-3x+m+2，在[0，2]上任取三个数a，b，c，均存在以f（a），f（b），f（c）为边的三角形，则实数m的范围是（ ）
| A、m＞2 | B、m＞4 |
| C、m＞6 | D、m＞8 |
等比数列{an}的前n项和为Sn，若S3+3S2=0，则公比q=（ ）
| A、-2 | B、2 | C、3 | D、-3 |
已知点P（cosα，tanα）在第三象限，则角α的终边在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若集合A={x|x≥0}，且A∩B=B，则集合B可能是（ ）
| A、{1，2} |
| B、{x|x≤1} |
| C、{-1，0，1} |
| D、R |
“|x-A|＜
，且|y-A|＜
”是“|x-y|＜?”（x，y，A，?∈R）的（ ）
| ? |
| 2 |
| ? |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若直线y=
x+2绕其与y轴的交点逆时针旋转
，则此时直线在x轴上的截距是（ ）
| 2 |
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
下列函数中，既是奇函数又是增函数的为（ ）
| A、y=x+1 | ||
| B、y=-x3 | ||
C、y=
| ||
| D、y=x|x| |
设函数f（x）=a+x-lnx有两个零点，则a的范围为（ ）
| A、[1，+∞） |
| B、（1，+∞） |
| C、（-∞，-1） |
| D、（-∞，1] |