题目内容
下列函数中，既是偶函数又在（0，+∞）上单调递增的是（ ）
| A、y=ln|x| |
| B、y=-x2 |
| C、y=ex |
| D、y=cosx |
考点：函数单调性的性质
专题：计算题,函数的性质及应用
分析：根据偶函数的定义，可得A，B，D是偶函数，再利用函数单调性的性质，即可得出结论．
解答：
解：根据偶函数的定义，可得A，B，D是偶函数，B在（0，+∞）上单调递减，D在（0，+∞）上有增有减，A在（0，+∞）上单调递增，
故选：A．
故选：A．
点评：本题考查函数单调性的性质，考查函数的奇偶性，考查学生分析解决问题的能力，比较基础．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
规定a?b=
+2a+b，a、b∈R+，若1?k=4，则函数f（x）=k?x的值域（ ）
| ab |
| A、（2，+∞） | ||
| B、（1，+∞） | ||
C、[
| ||
D、[
|
设函数f（x）的定义域为A，且满足任意x∈A恒有 f（x）+f（2-x）=2的函数可以是（ ）
A、f（x）=log2（x+
| ||
| B、f（x）=（x-2）3+1 | ||
C、f（x）=
| ||
| D、f（x）=（x-1）2 |
等比数列{an}的前n项和为Sn，若S3+3S2=0，则公比q=（ ）
| A、-2 | B、2 | C、3 | D、-3 |
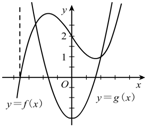
已知函数y=f（x）和y=g（x）的图象如图，则有（ ）
| A、f′（x）=g（x） |
| B、g′（x）=f（x） |
| C、f′（x）=g′（x） |
| D、g（x）=f（x） |
若集合A={x|x≥0}，且A∩B=B，则集合B可能是（ ）
| A、{1，2} |
| B、{x|x≤1} |
| C、{-1，0，1} |
| D、R |
已知盒中有10个灯泡，其中8个正品，2个次品．需要从中取出2个正品，每次取出1个，取出后不放回，直到取出2个正品为止．设ξ为取出的次数，求P（ξ=4）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|