题目内容
13.函数y=e-|lnx|-|2-x|的图象大致为( )| A. | 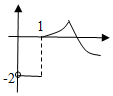 | B. | 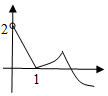 | C. | 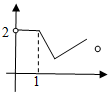 | D. | 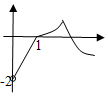 |
分析 写出函数在(0,1)上的解析式即可得出答案.
解答 解:当lnx≤0即0<x≤1时,y=elnx-|2-x|=x-(2-x)=2x-2,
∴函数y=e-|lnx|-|2-x|在(0,1]上单调递增,排除A,B,C,
故选D.
点评 本题考查了函数图象的判断,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知曲线$y=\frac{1}{4}{x^2}-3lnx$的一条切线的斜率为$-\frac{1}{2}$,则切点的横坐标为( )
| A. | -3 | B. | 2 | C. | -3或2 | D. | $\frac{1}{2}$ |
18.设复数z1,z2在复平面内的对应点关于实轴对称,z1=2+i,则z1z2=( )
| A. | 3 | B. | 5 | C. | -4+i | D. | 4+i |
2.函数$f(x)=\frac{1}{2}cos(ωx+φ)$(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则φ的值为( )
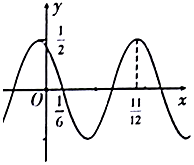

| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{3}$ |
3.已知向量$\overrightarrow{a}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),$\overrightarrow{b}$=($\sqrt{3}$,-1),则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
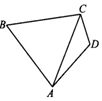 在△ABC中,角A、B、C所对的边分别为a,b,c,满足(2a-c)cosB=bcosC.
在△ABC中,角A、B、C所对的边分别为a,b,c,满足(2a-c)cosB=bcosC.