题目内容
16. 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
分析 由题意可得:设裁去四个全等的等腰三角形的底边边长为x,则图(2)中的底面正方形的边长=$\frac{12-x}{2}×\sqrt{2}$,又图(3)中的等边三角形的边长=$6\sqrt{2}$-$\frac{12-x}{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}(12+x)}{4}$.利用$\frac{\sqrt{2}}{2}$(12-x)=$\frac{\sqrt{2}(12+x)}{4}$.解得x,再利用体积计算公式即可得出.
解答 解:由题意可得:设裁去四个全等的等腰三角形的底边边长为x,则图(2)中的底面正方形的边长=$\frac{12-x}{2}×\sqrt{2}$,又图(3)中的等边三角形的边长=$6\sqrt{2}$-$\frac{12-x}{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}(12+x)}{4}$.
∴$\frac{\sqrt{2}}{2}$(12-x)=$\frac{\sqrt{2}(12+x)}{4}$.
解得x=4.
∴正四棱锥的体积=$\frac{1}{3}×(4\sqrt{2})^{2}$×$\frac{\sqrt{3}}{2}×4\sqrt{2}$=$\frac{64\sqrt{6}}{3}$.
故选:B.
点评 本题考查了空间位置关系、三视图、正四棱锥、等边三角形的性质、体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
4.在等比数列{an}中,a3a7=4a4=4,则a8等于( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
8.4个不同的小球全部随意放入3个不同的盒子里,使每个盒子都不空的放法种数为( )
| A. | C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$ | B. | A${\;}_{3}^{1}$A${\;}_{4}^{3}$ | ||
| C. | C${\;}_{4}^{3}$A${\;}_{2}^{2}$ | D. | ${C}_{4}^{2}{A}_{3}^{3}$ |
5.已知数列{an}中,a1=2,当n≥2时,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,设bn=$\frac{{a}_{n}}{{2}^{n}}$-1,则$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$等于( )
| A. | $\frac{19}{10}$ | B. | $\frac{29}{20}$ | C. | $\frac{40}{21}$ | D. | $\frac{36}{19}$ |
6.下列函数中,图象的一部分符合右图的是( )
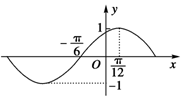

| A. | $y=sin(x+\frac{π}{6})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(2x+\frac{π}{6})$ | D. | $y=sin(2x+\frac{π}{3})$ |
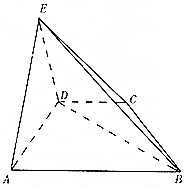 如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.
如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.