题目内容
1.三进制数2022(3)化为六进制数为abc(6),则a+b+c=7.分析 先将2022(3)转化为“十进制”数,再转化为6进制数是142(6),从而可求a+b+c的值.
解答 解:“五进制”数为2022(3)转化为“十进制”数为:2×33+0×32+2×31+2=62.
将十进制数62转化为6进制数:
62÷6=10…2,
10÷6=1…4,
1÷6=0…1,
∴将十进制62化为6进制数是142(6),
则a+b+c=7,
故答案为:7.
点评 本题考查进位制,本题解题的关键是理解进位制之间的转化原则,注意数字的运算不要出错,本题是一个基础题.

练习册系列答案
相关题目
17.在平面直角坐标系xOy中,以坐标原点为圆心且与直线mx-y-2m+1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为( )
| A. | x2+y2=5 | B. | x2+y2=3 | C. | x2+y2=9 | D. | x2+y2=7 |
9.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am、an使得$\sqrt{{a}_{m}{a}_{n}}$=4a1,则$\frac{1}{m}$+$\frac{4}{n}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{25}{6}$ | D. | $\frac{4}{3}$ |
16. 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
6.下列求导运算正确的是( )
| A. | (log2x)′=$\frac{1}{xln2}$ | B. | ($\frac{cosx}{x}$)′=$\frac{xsinx-cosx}{x}$ | ||
| C. | (10x)′=10xlge | D. | (x+$\sqrt{x}$)′=1-$\frac{1}{2\sqrt{x}}$ |
13.如图所示给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,其中判断框内应填入的条件是( )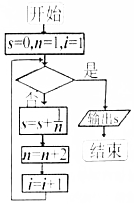

| A. | i>1010 | B. | i<1010 | C. | i>1009 | D. | i<1009 |
10.某数学兴趣小组有3名男生和2名女生,从中任选出2名同学参加数学竞赛,那么对立的两个事件为( )
| A. | 恰有1名女生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名女生与全是男生 |