题目内容
6.已知圆锥曲线C:$\left\{\begin{array}{l}{x=2cosα}\\{y=\sqrt{3}sinα}\end{array}\right.$(α是参数)和定点A(0,$\sqrt{3}$),F1,F2分别是曲线C的左、右焦点.(1)以原点为极点,x轴的正半轴为极轴建立坐标系,求直线AF2的极坐标系方程.
(2)若P是曲线C上的动点,求|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|的取值范围.
分析 (1)求出直线AF2的直角坐标方程,再转化为极坐标方程;
(2)根据椭圆的性质得|$\overrightarrow{P{F}_{1}}$|=4-|$\overrightarrow{P{F}_{2}}$|,将利|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|转化为二次函数求出最值.
解答 解:(1)曲线C的普通方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,∴F2(1,0),
∴直线AF2的斜率k=-$\sqrt{3}$,∴直线AF2的直角坐标方程为y=-$\sqrt{3}x$+$\sqrt{3}$.
∴直线AF2的极坐标方程为ρsinθ=-$\sqrt{3}ρ$cosθ+$\sqrt{3}$.
(2)P是曲线C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$上的动点,∴1≤|$\overrightarrow{P{F}_{2}}$|≤3.
∵|$\overrightarrow{P{F}_{1}}$|+|$\overrightarrow{P{F}_{2}}$|=4,∴|$\overrightarrow{P{F}_{1}}$|=4-|$\overrightarrow{P{F}_{2}}$|,
∴|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=|$\overrightarrow{P{F}_{1}}$|×(4-|$\overrightarrow{P{F}_{2}}$|)=-|$\overrightarrow{P{F}_{2}}$|2+4|$\overrightarrow{P{F}_{1}}$|=-($\overrightarrow{P{F}_{2}}$-2)2+4.
∴当|$\overrightarrow{P{F}_{2}}$|=2时,|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|取得最大值4,当|$\overrightarrow{P{F}_{2}}$|=1或3时,|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|取得最小值3.
∴|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|的取值范围是[3,4].
点评 本题考查了参数方程,极坐标方程与普通方程的转化,椭圆的几何性质,属于基础题.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | (-4,-3) | B. | (4,3) | C. | (-4,3) | D. | (3,4) |
| A. | 0∉N | B. | $0•\overrightarrow{AB}=0$ | C. | cos0.75°>cos0.7 | D. | lge>(lge)2>lg$\sqrt{e}$ |
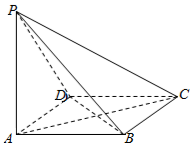 如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$.