题目内容
14.求y=4-3sin(2x-$\frac{π}{4}$)的最小正周期、最大值、最小值,并求出y取最大值、最小值时x的值.分析 结合正弦函数的图象与性质求出周期,最值,列出方程解出x.
解答 解:函数y=4-3sin(2x-$\frac{π}{4}$)的最小正周期T=$\frac{2π}{2}$=π.
当sin(2x-$\frac{π}{4}$)=-1时,y取得最大值4+3=7;此时2x-$\frac{π}{4}$=-$\frac{π}{2}+2kπ$,解得x=-$\frac{π}{8}$+kπ,k∈Z.
当sin(2x-$\frac{π}{4}$)=1时,y取得最小值4-3=1;此时2x-$\frac{π}{4}$=$\frac{π}{2}+2kπ$,解得x=$\frac{3π}{8}$+kπ,k∈Z.
点评 本题考查了正弦函数的图象与性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知奇函数f(x)=ax3+bx2+2x+c,且f(1)=5,则f(2)=( )
| A. | -5 | B. | 10 | C. | 25 | D. | 28 |
3.某四棱锥的三视图如图所示,该四棱锥外接球的表面积为( )
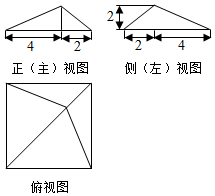

| A. | 72π | B. | 100π | C. | 108π | D. | 72$\sqrt{2}π$ |