题目内容
12.设f(x)是R上的奇函数,且当x∈(0,+∞)时,f(x)=x(x+1),则当x∈(-∞,0)时,f(x)的解析式为f(x)=x(1-x).分析 设x<0,则-x>0,由已知表达式可求f(-x),根据奇函数性质可得f(x)与f(-x)的关系式,由此即可得到答案.
解答 解:设x<0,则-x>0,
∴f(-x)=-x(1-x),
又f(x)为R上的奇函数,
所以f(x)=-f(-x),
即f(x)=-[-x(1-x)]=x(1-x),
故答案为:f(x)=x(1-x).
点评 本题考查函数解析式的求法及函数奇偶性的性质,考查学生灵活运用知识解决问题的能力,属基础题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.某四棱锥的三视图如图所示,该四棱锥外接球的表面积为( )
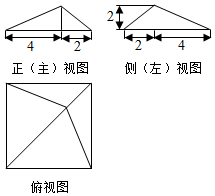

| A. | 72π | B. | 100π | C. | 108π | D. | 72$\sqrt{2}π$ |
7.函数f(x)=-x2+3x-a,g(x)=2x-x2,若f[g(x)]≥0对x∈[0,1]恒成立,则实数a的范围是( )
| A. | (-∞,2] | B. | (-∞,e] | C. | (-∞,ln2] | D. | [0,$\frac{1}{2}$) |
3.点(5,-3)到直线x+2=0的距离等于( )
| A. | 7 | B. | 5 | C. | 3 | D. | 2 |