题目内容
18.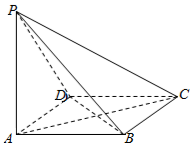 如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$. (Ⅰ)求证:平面PBD⊥平面PAC;
(Ⅱ)求三棱锥P-BDC的体积.
分析 (Ⅰ)通过证BD⊥AC,BD⊥PA,得出BD⊥平面PAC,又BD在平面PBD内,推出平面PBD⊥平面PAD.
(Ⅱ)直接利用V=$\frac{1}{3}$S△BDC•PA,求解几何体的体积.
解答 (Ⅰ)证明:因为四棱锥P-ABCD的底面为菱形,所以BD⊥AC,
又PA⊥底面ABCD,BD?平面ABCD,所以BD⊥PA,
因为PA∩AC=A,
所以BD⊥平面PAC,
又BD在平面PBD内,
所以平面PBD⊥平面PAD.…(6分)
(Ⅱ)解:因为PA⊥底面ABCD,所以PA是底面BCD上的高,
所以:$V=\frac{1}{3}{S_{△BDC}}•PA=\frac{1}{3}×(\frac{1}{2}×2×2×\frac{{\sqrt{3}}}{2})×\sqrt{3}=1$.…(12分)
点评 本题考查空间想象能力,直线与平面垂直,平面与平面垂直,几何体的体积的计算,属于中档题.

练习册系列答案
相关题目
7.函数f(x)=-x2+3x-a,g(x)=2x-x2,若f[g(x)]≥0对x∈[0,1]恒成立,则实数a的范围是( )
| A. | (-∞,2] | B. | (-∞,e] | C. | (-∞,ln2] | D. | [0,$\frac{1}{2}$) |
3.点(5,-3)到直线x+2=0的距离等于( )
| A. | 7 | B. | 5 | C. | 3 | D. | 2 |
8.复数$\frac{{|{4+3i}|}}{3-4i}$(i为虚数单位)的共轭复数对应的点位于复平面内( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |