题目内容
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.
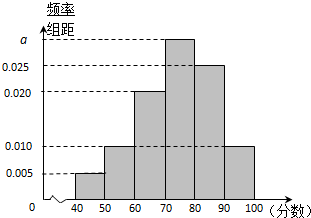
(Ⅰ)求图中实数a的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.

(Ⅰ)求图中实数a的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:图表型,概率与统计
分析:(I)根据频率=小矩形的高×组距,利用数据的频率之和为1求得a值;
(II)由频率分布直方图求得数学成绩不低于60分的概率,利用频数=样本容量×频率计算;
(III)用列举法写出从第一组和第六组6名学生中选两名学生的所有结果,从中找出数学成绩之差的绝对值不大于10的结果,利用个数之比求概率.
(II)由频率分布直方图求得数学成绩不低于60分的概率,利用频数=样本容量×频率计算;
(III)用列举法写出从第一组和第六组6名学生中选两名学生的所有结果,从中找出数学成绩之差的绝对值不大于10的结果,利用个数之比求概率.
解答:
解:(Ⅰ)根据数据的频率之和为1,得0.05+0.1+0.2+10a+0.25+0.1=1,
∴a=0.03;

(Ⅱ)数学成绩不低于60分的概率为:0.2+0.3+0.25+0.1=0.85,
∴数学成绩不低于60分的人数为500×0.85=425人
(Ⅲ)数学成绩在[40,50)的学生人数:40×0.005×10=2人,
数学成绩在[50,60)的学生人数:40×0.01×10=4人,
设数学成绩在[40,50)的学生为A,B;
数学成绩在[90,100)的学生为a,b,c,d;
从6名学生中选两名学生的结果有:{A,B},{A,a},{A,b},{A,c},{A,d},{B,a},{B,b},{B,c},{B,d},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d}.共15种;
其中两名学生的数学成绩之差的绝对值不大于10的情况有:{A,B},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d}共7种;
∴抽取的两名学生的数学成绩之差的绝对值不大于10的概率为
.
∴a=0.03;

(Ⅱ)数学成绩不低于60分的概率为:0.2+0.3+0.25+0.1=0.85,
∴数学成绩不低于60分的人数为500×0.85=425人
(Ⅲ)数学成绩在[40,50)的学生人数:40×0.005×10=2人,
数学成绩在[50,60)的学生人数:40×0.01×10=4人,
设数学成绩在[40,50)的学生为A,B;
数学成绩在[90,100)的学生为a,b,c,d;
从6名学生中选两名学生的结果有:{A,B},{A,a},{A,b},{A,c},{A,d},{B,a},{B,b},{B,c},{B,d},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d}.共15种;
其中两名学生的数学成绩之差的绝对值不大于10的情况有:{A,B},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d}共7种;
∴抽取的两名学生的数学成绩之差的绝对值不大于10的概率为
| 7 |
| 15 |
点评:本题主要是考查了直方图以及古典概型概率的计算,在频率分布直方图中频率=小矩形的面积=小矩形的高×组距,用列举法写出所有基本事件是求古典概型概率的常用方法..

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
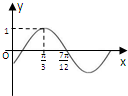 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
 如图,△ABC的三条角平分线交于点O,过点O作OE⊥BC于点E,求证:∠BOD=∠COE.
如图,△ABC的三条角平分线交于点O,过点O作OE⊥BC于点E,求证:∠BOD=∠COE.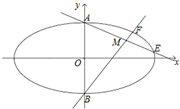 已知椭圆Γ:
已知椭圆Γ: