题目内容
当a＞0，b＞0时，不等式
+
≥
，则λ的最大值为 ．
| 2 |
| a |
| 1 |
| b |
| λ |
| a+2b |
考点：基本不等式
专题：不等式的解法及应用
分析：根据基本不等式的性质a+b≥2
，化简计算即可．
| ab |
解答：
解：∵
+
≥
，a＞0，b＞0
∴(a+2b)(
+
)≥λ，
∵(a+2b)(
+
)=4+
+
≥4+2
=8，
∴λ≤8，
∴λ的最大值为8．
故答案为：8．
| 2 |
| a |
| 1 |
| b |
| λ |
| a+2b |
∴(a+2b)(
| 2 |
| a |
| 1 |
| b |
∵(a+2b)(
| 2 |
| a |
| 1 |
| b |
| 4b |
| a |
| a |
| b |
|
∴λ≤8，
∴λ的最大值为8．
故答案为：8．
点评：本题主要考查了基本不等式的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设复数ω=-
+
i（i为虚数单位），则（ω+1）2=（ ）
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
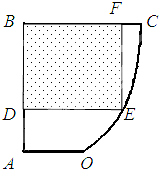某同学的数学研究性学习课题是：在校内一块不规则土地OABC（测绘图如图所示）规划一个矩形运动场地．经过测量发现AB⊥BC，OA∥BC，曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段，OA=20m，AB=BC=40m．