题目内容
7．将5名教师分到3个班任课，每班至少分1名，有多少种不同的分法？分析 根据题意，分两种情况讨论：①将5名教师分成三组，一组1人，另两组都是2人，②将5名教师分成三组，一组3人，另两组都是1人，由组合数公式计算可得每种情况下的分配方案数目，由分类计数原理计算可得答案．
解答 解：将5名教师分到3个班任课，每班至少分1名，有2种情况：
①将5名教师分成三组，一组1人，另两组都是2人，有$\frac{{C}_{5}^{1}{C}_{4}^{2}}{{A}_{2}^{2}}$=15种分组方法，
再将3组分到3个班，共有15•A33=90种不同的分配方案，
②将5名教师分成三组，一组3人，另两组都是1人，有$\frac{{C}_{5}^{3}{C}_{2}^{1}}{{A}_{2}^{2}}$=10种分组方法，
再将3组分到3个班，共有10•A33=60种不同的分配方案，
共有90+60=150种不同的分配方案．
点评 本题考查排列、组合的运用，注意先要根据题意要求，进行分类讨论，其次要正确运用分组公式
练习册系列答案
阶梯计算系列答案
相关题目
18．海上有相距10海里的A与B两个小岛，从A岛望另外一个C岛和B岛成60°的视角，从B岛望C岛和A岛成75°的视角，则B与C之间的距离是（ ）
| A． | $10\sqrt{3}$海里 | B． | $\frac{{10\sqrt{6}}}{3}$海里 | C． | $5\sqrt{2}$ 海里 | D． | $5\sqrt{6}$海里 |
2．东莞某家具生产厂家根据市场调查分析，决定调整新产品生产方案，准备每周（按40个工时计算）生产书桌、书柜、电脑椅共120张，且书桌至少生产20张．已知生产这些家具每张所需工时和每张产值如表：
问每周应生产书桌、书柜、电脑椅各多少张，才能使产值最高？最高产值是多少？（以千元为单位）
| 家具名称 | 书桌 | 书柜 | 电脑椅 |
| 工 时 | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 产值（千元） | 4 | 3 | 2 |
12．使函数y=sinx为增函数，且函数值为负数的区间是（ ）
| A． | （0，$\frac{π}{2}$） | B． | （$\frac{π}{2}$，π） | C． | （π，$\frac{3π}{2}$） | D． | （$\frac{3π}{2}$，2π） |
19．在三角形中，角A，B，C的对边分别为a，b，c，若2sinAcosC=sinB，则$\frac{a}{c}$的值是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
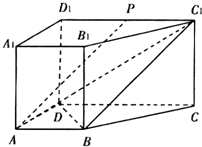如图，直四棱柱ABCD-A1B1C1D1中，AB∥CD，AD⊥AB，AB=AD=$\frac{1}{2}$CD=1．点P为线段C1D1的中点．