Question

19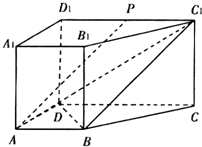．如图，直四棱柱ABCD-A₁B₁C₁D₁中，AB∥CD，AD⊥AB，AB=AD=$\frac{1}{2}$CD=1．点P为线段C₁D₁的中点．
（Ⅰ）求证：AP∥平面BDC₁；
（Ⅱ）求证：平面BCC₁⊥平面BDC₁．

Answer 1

分析 （Ⅰ）推导出四边形ABC₁P为平行四边形，从而AP∥BC₁，由此能证明AP∥平面BDC₁．
（Ⅱ）推导出BD⊥BC，CC₁⊥BD，从而BD⊥平面BCC₁．由此能证明平面BCC₁⊥平面BDC₁．

解答 证明：（Ⅰ）∵点P是线段C₁D₁的中点，∴PC₁=$\frac{1}{2}{D}_{1}{C}_{1}$，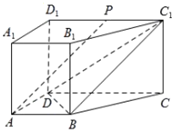
由题意PC₁∥DC，∴PC₁$\underset{∥}{=}$$\frac{1}{2}DC$，
又AB$\underset{∥}{=}$$\frac{1}{2}DC$，∴PC₁$\underset{∥}{=}$AB，
∴四边形ABC₁P为平行四边形，
∴AP∥BC₁，
又∵AP?平面BDC₁，BC₁?平面BDC₁，
∴AP∥平面BDC₁．
（Ⅱ）在底面ABCD中，
∵AB∥CD，AD⊥AB，AB=AD=$\frac{1}{2}CD=1$，
∴BD=BC=$\sqrt{2}$，
在△BCD中，BD²+BC²=CD²，∴BD⊥BC，
由已知CC₁⊥底面ABCD，∴CC₁⊥BD，
又BC∩CC₁=C，∴BD⊥平面BCC₁．
又∵BD?平面BDC₁，∴平面BCC₁⊥平面BDC₁．

点评 本题考查线面平行的证明，考查面面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．