题目内容
10.实系数一元二次方程x2+ax+b=0的一个根在(0,1)上,另一个根在(1,2)上,则$\frac{2-b}{2-a}$的取值范围是( )| A. | (0,$\frac{2}{3}$) | B. | (-∞,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,2) | D. | $(\frac{2}{3},+∞)$ |
分析 利用一元二次方程根的分布与系数的关系,二次函数的性质,求得a、b满足的条件,画出它的可行域,而$\frac{2-b}{2-a}$表示可行域内的点与点M(2,2)连线的斜率,数形结合可得$\frac{2-b}{2-a}$的取值范围.
解答 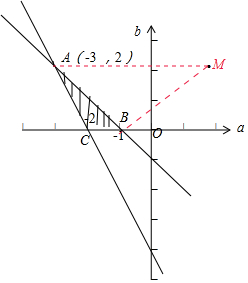 解:∵实系数一元二次方程x2+ax+b=0的一个根在(0,1)上,另一个根在(1,2)上,
解:∵实系数一元二次方程x2+ax+b=0的一个根在(0,1)上,另一个根在(1,2)上,
∴$\left\{\begin{array}{l}{f(0)=b>0}\\{f(1)=1+a+b<0}\\{f(2)=4+2a+b>0}\end{array}\right.$,画出它的可行域,如图所示:△ABC的内部.
而$\frac{2-b}{2-a}$表示可行域内的点与点M(2,2)连线的斜率,
而直线MA的斜率为0,直线MB的斜率为$\frac{2-0}{2+1}$=$\frac{2}{3}$,
故$\frac{2-b}{2-a}$的取值范围是(0,$\frac{2}{3}$),
故选:A.
点评 本题主要考查实系数一元二次方程根的分布与系数的关系,二次函数的性质,直线的斜率公式,简单的线性规划问题,属于中档题.

练习册系列答案
相关题目
1.执行如图所示程序框图,则输出的S的值为( )


| A. | 4 | B. | 8 | C. | -20 | D. | -4 |
18.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{3}$|$\overrightarrow{b}$|,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$-3$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
5.函数f(x)=(2x-1)ex的递增区间为( )
| A. | (-∞,+∞) | B. | $({\frac{1}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-\frac{1}{2},+∞})$ |
18.若复数Z满足Z(i-1)=2i(i为虚数单位),则$\overline{z}$为( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
19.给出下面的语句:最后输出的结果是( )


| A. | 1+2+3+…+100 | B. | 12+22+32+…+1002 | C. | 1+3+5+…+99 | D. | 12+32+52+…+992 |