题目内容
若函数f(x)对任意x∈R满足f(x)+1=
,且x∈(0,1)时,f(x)=x,g(x)=f(x)-mx-m在(-1,0)∪(0,1)上有两个零点,则实数m的取值范围是( )
| 1 |
| f(x+1) |
| A、(-1,1) | ||
B、(0,
| ||
| C、(0,1) | ||
| D、(-1,2] |
考点:函数的零点
专题:函数的性质及应用
分析:根据f(x)+1=
,当x∈[0,1]时,f(x)=x,求出x∈(-1,0)时,f(x)的解析式,由在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,转化为两函数图象的交点,利用图象直接的结论.
| 1 |
| f(x+1) |
解答:
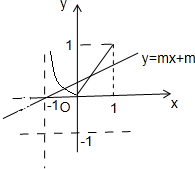 解:∵x∈(0,1)时,f(x)=x,
解:∵x∈(0,1)时,f(x)=x,
∴当x∈(-1,0)时,x+1∈(0,1),∴
f(x+1)=x+1=
,
∴f(x)=
-1,
∴函数f(x)=
∵g(x)=f(x)-mx-m有两个零点,
所以y=f(x)与y=mx+m的图象有两个交点,
函数图象如图,
由图得,当0<m<
时,两函数有两个交点,
故实数m的取值范围是(0,
),
故选:B
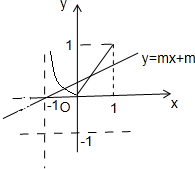 解:∵x∈(0,1)时,f(x)=x,
解:∵x∈(0,1)时,f(x)=x,∴当x∈(-1,0)时,x+1∈(0,1),∴
f(x+1)=x+1=
| 1 |
| f(x)+1 |
∴f(x)=
| 1 |
| x+1 |
∴函数f(x)=
|
∵g(x)=f(x)-mx-m有两个零点,
所以y=f(x)与y=mx+m的图象有两个交点,
函数图象如图,
由图得,当0<m<
| 1 |
| 2 |
故实数m的取值范围是(0,
| 1 |
| 2 |
故选:B
点评:此题是个中档题.本题考查了利用函数零点的存在性求变量的取值范围和代入法求函数解析式,体现了转化的思想,以及利用函数图象解决问题的能力,体现了数形结合的思想.也考查了学生创造性分析解决问题的能力.

练习册系列答案
相关题目
已知等比数列{an},a4+a8=∫
dx,则a6(a2+2a6+a10)的值为( )
2 0 |
| 4-x2 |
| A、π2 | B、π |
| C、4 | D、-9π |
定义:在数列{an}中,若满足
-
=d(n∈N+,d 为常数),称{an}为“等差比数列”.已知在“等差比数列”{an}中,a1=a2=1,a3=3,则
=( )
| an+2 |
| an+1 |
| an+1 |
| an |
| a2014 |
| a2012 |
| A、4×20122-1 |
| B、4×20132-1 |
| C、4×20142-1 |
| D、4×20132 |
若存在过点(1,1)的直线与曲线y=x2+x和y=ax2-x-1都相切,则a等于( )
| A、-1或-3 | B、-2或3 |
| C、-1或3 | D、1或-3 |
设随机变量ξ服从正态分布N(3,4),若P(ξ<2a-2)=P(ξ>a+2),则a=( )
| A、4 | B、3 | C、2 | D、1 |