题目内容
若存在过点（1，1）的直线与曲线y=x2+x和y=ax2-x-1都相切，则a等于（ ）
| A、-1或-3 | B、-2或3 |
| C、-1或3 | D、1或-3 |
考点：利用导数研究曲线上某点切线方程
专题：综合题,导数的综合应用
分析：设出所求切线方程的切点坐标和斜率，把切点坐标代入曲线方程得到一个等式，根据切点坐标和斜率写出切线的方程，把切点坐标代入又得到一个等式，联立方程组即可求出切点的横坐标，进而得到切线的斜率，根据已知点的坐标和求出的斜率写出切线方程，再根据与y=y=ax2-x-1相切，联立方程组，△=0可求出所求．
解答：
解：设直线与曲线y=x2+x的切点坐标为（x0，y0），
则
，则切线的斜率k=1或k=5，
若k=1，此时切线的方程为y=x，
由y=x与y=ax2-x-1，消去y，可得ax2-2x-1=0，
其中△=0，解可得a=-1；
若k=5，其切线方程为y=5x-4，
由y=5x-4与y=ax2-x-1，消去y可得ax2-6x+3=0，
又由△=0，即36-12a=0，
解可得a=3．
故a=3或-1．
故选：C．
则
|
若k=1，此时切线的方程为y=x，
由y=x与y=ax2-x-1，消去y，可得ax2-2x-1=0，
其中△=0，解可得a=-1；
若k=5，其切线方程为y=5x-4，
由y=5x-4与y=ax2-x-1，消去y可得ax2-6x+3=0，
又由△=0，即36-12a=0，
解可得a=3．
故a=3或-1．
故选：C．
点评：本题主要考查了导数的几何意义，以及利用导数求曲线上过某点切线方程的斜率，会根据一点坐标和斜率写出直线的方程，是一道综合题．
练习册系列答案
相关题目
复数
的共轭复数是（ ）
| i+1 |
| 1-i |
| A、2 | B、i | C、-i | D、-2i |
设a，b，c分别是△ABC中角A，B，C的对边边长，且lgsinA，lgsinB，lgsinC成等差数列，则直线l1：xsin2A+ysinA-a=0与直线l2：xsin2B+ysinC-c=0的位置关系是（ ）
| A、平行 | B、重合 |
| C、垂直 | D、相交但不垂直 |
若函数f（x）对任意x∈R满足f（x）+1=
，且x∈（0，1）时，f（x）=x，g（x）=f（x）-mx-m在（-1，0）∪（0，1）上有两个零点，则实数m的取值范围是（ ）
| 1 |
| f(x+1) |
| A、（-1，1） | ||
B、（0，
| ||
| C、（0，1） | ||
| D、（-1，2] |
已知i是虚数单位，复数
的模为（ ）
| -5+i |
| 2-3i |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
直线l1过点A（2，-1）和点B（3，2），直线l2的倾斜角是直线l1的倾斜角的两倍，则直线l2的斜率为（ ）
| A、-6 | ||
B、-
| ||
C、
| ||
D、-
|
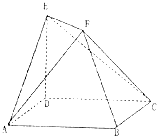如图，底面ABCD是边长为4的正方形，ED⊥平面ABCD，ED=2，EF∥BD，且2EF=BD．