题目内容
已知抛物线C:y2=2px的焦点坐标F(1,0),过F的直线L交抛物线C于A、B两点,直线AO、BO分别与直线m:x=-2相交于M、N.
(1)求抛物线C方程.
(2)求
的值.
(1)求抛物线C方程.
(2)求
| S△ABO |
| S△MNO |
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据焦点的坐标,求得P即可;
(2)根据直线L与x轴是否垂直,分两种情况求解△ABO与△MNO的面积之比,验证即可.
(2)根据直线L与x轴是否垂直,分两种情况求解△ABO与△MNO的面积之比,验证即可.
解答:
解:(1)∵抛物线C:y2=2px的焦点坐标F(1,0),
∴抛物线C方程为y2=4x.
(2)当直线l垂直于x轴时,△ABO与△MNO相似,
∴
=(
)2=
.
当直线l与x轴不垂直时,设直线AB方程为y=k(x-1),
设M(-2,yM),N(-2,yN),A(x1,y1),B(x2,y2),
解
整理得k2x2-(4+2k2)x+k2=0,
∵∠AOB=∠MON,
∴x1•x2=1.∴
=
=
•
=
.
综上
=
.
∴抛物线C方程为y2=4x.
(2)当直线l垂直于x轴时,△ABO与△MNO相似,
∴
| S△ABO |
| S△MNO |
| |OF| |
| 2 |
| 1 |
| 4 |
当直线l与x轴不垂直时,设直线AB方程为y=k(x-1),
设M(-2,yM),N(-2,yN),A(x1,y1),B(x2,y2),
解
|
∵∠AOB=∠MON,
∴x1•x2=1.∴
| S△ABO |
| S△MNO |
| ||
|
| AO |
| MO |
| BO |
| NO |
| 1 |
| 4 |
综上
| S△ABO |
| S△MNO |
| 1 |
| 4 |
点评:本题考查直线与圆锥曲线的关系及抛物线的标准方程.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若函数f(x)对任意x∈R满足f(x)+1=
,且x∈(0,1)时,f(x)=x,g(x)=f(x)-mx-m在(-1,0)∪(0,1)上有两个零点,则实数m的取值范围是( )
| 1 |
| f(x+1) |
| A、(-1,1) | ||
B、(0,
| ||
| C、(0,1) | ||
| D、(-1,2] |
已知m,n∈R则“m>0且n>0”是“曲线
+
=1为椭圆”的( )
| x2 |
| m |
| y2 |
| n |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列四个函数中,既是定义域上的奇函数又在区间(0,1)内单调递增的是( )
A、y=
| ||
| B、y=xsinx | ||
C、y=lg
| ||
| D、y=ex-e-x |
已知向量
=(3,4),
=(-1,5),向量k
+2
与向量
=(2,-3)垂直,则k的值是( )
| a |
| b |
| a |
| b |
| c |
| A、2 | ||
B、-
| ||
| C、1 | ||
| D、-3 |
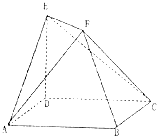 如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD.
如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD. 已知点P是射线y=2(x>1)上一点.过P作直线MN,交抛物线y2=4x于M,N两点,使点P平分线段MN.
已知点P是射线y=2(x>1)上一点.过P作直线MN,交抛物线y2=4x于M,N两点,使点P平分线段MN.