题目内容
已知定义域为R的函数f(x)为奇函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(log 24)的值.
24)的值.
(1)令x∈[-1,0),则-x∈(0,1],
∴f(-x)=2-x-1.又∵f(x)是奇函数,
∴f(-x)=-f(x),
∴-f(x)=f(-x)=2-x-1,
∴f(x)=- x+1.
x+1.
(2)∵log 24=-log224∈(-5,-4),
24=-log224∈(-5,-4),
∴log 24+4∈(-1,0),
24+4∈(-1,0),
∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
∴f(x)是以4为周期的周期函数,
∴f(log 24)=f(log
24)=f(log 24+4)
24+4)
=- log
log 24+4+1
24+4+1
=-24× +1=-
+1=-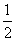 .
.

练习册系列答案
相关题目
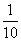 ,1),a=lgx,b=lg2x,c=
,1),a=lgx,b=lg2x,c=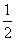 lgx,则a、b、c的大小关系是( )
lgx,则a、b、c的大小关系是( ) 的大小关系是( )
的大小关系是( )
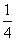 B.
B. 的图像大致是( )
的图像大致是( )