题目内容
下列结论:
①若命题p:?x∈R,tanx=1;命题q:?x∈R,x2-x+1>0则命题“p∧¬q”是假命题.
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是
=-3
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.
④命题p:a>1,b>1,命题q:ab>1,则p是q的充分条件
其中正确命题的个数为 ( )
①若命题p:?x∈R,tanx=1;命题q:?x∈R,x2-x+1>0则命题“p∧¬q”是假命题.
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是
| a |
| b |
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.
④命题p:a>1,b>1,命题q:ab>1,则p是q的充分条件
其中正确命题的个数为 ( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:分别判断命题p与q的真假,进而根据复合命题真假判断的真值表,判断①;根据线段垂直的充要条件,可判断②;写出原命题的逆否命题可判断③;根据充分条件的定义,可判断④.
解答:
解:对于①,?x=
∈R,使tanx=1,故命题p为真;由x2-x+1=0的
,可得?x∈R,x2-x+1>0,故命题q为真,则¬q为假,则命题“p∧¬q”是假命题.即①正确;
对于②,已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是a+3b=0,不是
=-3,故②错误;
对于③,命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.故③正确;
对于④,命题p:a>1,b>1,命题q:ab>1,则p是q的充分条件,故④正确;
故正确的命题有3个,
故选:D
| π |
| 4 |
|
对于②,已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是a+3b=0,不是
| a |
| b |
对于③,命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.故③正确;
对于④,命题p:a>1,b>1,命题q:ab>1,则p是q的充分条件,故④正确;
故正确的命题有3个,
故选:D
点评:本题以命题的真假判断为载体,考查了复合命题,充要条件,四种命题,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知球的半径为R,则半球的最大内接正方体的边长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、(
|
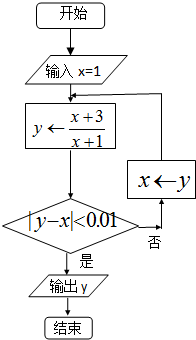 毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数x,x≠
毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数x,x≠