题目内容
 如图所示,两定点A(-6,0),B(2,0),O为坐标原点,动点P对线段AO,BO所张的角相等(即∠APO=∠BPO),求动点P的轨迹方程.
如图所示,两定点A(-6,0),B(2,0),O为坐标原点,动点P对线段AO,BO所张的角相等(即∠APO=∠BPO),求动点P的轨迹方程.考点:轨迹方程
专题:直线与圆
分析:设动点P(x,y),由∠APO=∠BPO,根据角平分线定理得
=3列出等式,化简整理即得.但应注意曲线上的点与方程的解对应的点是否一一对应.
| |PA| |
| |PB| |
解答:
解:如图,
设动点P(x,y),由动点P对线段AO、OB所张角相等,得∠APO=∠BPO,
由角平分线定理,得
=
.
∴
=3.整理得x2+y2-6x=0.
由方程可知圆过原点,但当P和原点重合时无意义,∴x≠0.
∴所求方程为x2+y2-6x=0(x≠0).
又由题意可知P点落在x轴上除线段AB以外的任何点处均有∠APO=∠BPO=0°,
∴又有方程y=0(x<-6或x>2).
故动点P的轨迹方程为x2+y2-6x=0(x≠0)或y=0(x<-6或x>2).

设动点P(x,y),由动点P对线段AO、OB所张角相等,得∠APO=∠BPO,
由角平分线定理,得
| |PA| |
| |PB| |
| |AO| |
| |BO| |
∴
| ||
|
由方程可知圆过原点,但当P和原点重合时无意义,∴x≠0.
∴所求方程为x2+y2-6x=0(x≠0).
又由题意可知P点落在x轴上除线段AB以外的任何点处均有∠APO=∠BPO=0°,
∴又有方程y=0(x<-6或x>2).
故动点P的轨迹方程为x2+y2-6x=0(x≠0)或y=0(x<-6或x>2).
点评:求轨迹方程时经常遇到“去”和“补”的问题,当所求的方程包括不合题意的点时,必须去掉,当所求的方程不含其他合乎条件的点时,必须补出来,此题是中档题.

练习册系列答案
相关题目
点p(x,y)满足5
=|3x-4y+5|,则点p的轨迹是( )
| (x-1)2+(y-2)2 |
| A、直线 | B、椭圆 |
| C、双曲线 | D、抛物线 |
 已知三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为
已知三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为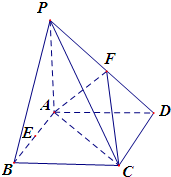 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是正方形,E,F分别是AB,PD的中点,且PA=AB=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是正方形,E,F分别是AB,PD的中点,且PA=AB=2.