题目内容
计算：tan10°tan40°+tan10°tan60°-tan60°tan40°．
考点：两角和与差的正切函数
专题：三角函数的求值
分析：由tan（40°+60°）=
变形，代入要求的式子化简可得．
| tan40°+tan60° |
| 1-tan40°tan60° |
解答：
解：∵tan（40°+60°）=
，
∴tan10°tan40°+tan10°tan60°-tan60°tan40°
=tan10°（tan40°+tan60°）-tan60°tan40°
=tan10°（tan40°+60°）（1-tan60°tan40°）-tan60°tan40°
=tan10°tan100°（1-tan60°tan40°）-tan60°tan40°
=-tan10°tan80°（1-tan60°tan40°）-tan60°tan40°
=-tan10°•
（1-tan60°tan40°）-tan60°tan40°
=-1+tan60°tan40°-tan60°tan40°
=-1
| tan40°+tan60° |
| 1-tan40°tan60° |
∴tan10°tan40°+tan10°tan60°-tan60°tan40°
=tan10°（tan40°+tan60°）-tan60°tan40°
=tan10°（tan40°+60°）（1-tan60°tan40°）-tan60°tan40°
=tan10°tan100°（1-tan60°tan40°）-tan60°tan40°
=-tan10°tan80°（1-tan60°tan40°）-tan60°tan40°
=-tan10°•
| 1 |
| tan10° |
=-1+tan60°tan40°-tan60°tan40°
=-1
点评：本题考查两角和与差的正切函数，正确变形是解决问题的关键，属基础题．
练习册系列答案
相关题目
在等差数列{an}中，已知a5+a7=16，则该数列前11项和S11的值是（ ）
| A、88 | B、58 |
| C、143 | D、176 |
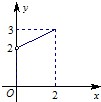已知函数f（x）是定义在[-2，0）∪（0，2]上的奇函数，当x＞0时，f（x）的图象如图所示．